Anello di M÷bius
L'anello o nastro di M÷bius, dal nome del matematico tedesco August Ferdinand M÷bius, Ŕ un esempio di superficie non orientabile. Ci˛ significa che non potremo in alcun modo distinguere un "fuori" e un "dentro", o un "sopra" e un "sotto", ma esiste un solo lato e un solo bordo.
Se infatti scorriamo con un dito la sua superficie, dopo aver percorso un giro ci troviamo dalla parte opposta a quella di partenza, mentre dopo averne percorsi due torniamo alla posizione iniziale.
Una dimostrazione visiva Ŕ data dall'animazione accanto.
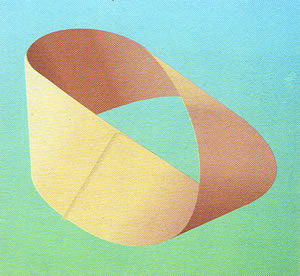
Un nastro di M÷bius pu˛ essere facilmente realizzato partendo da una striscia rettangolare ed unendone i lati corti dopo aver impresso ad uno di essi mezzo giro di torsione, pari a 180░.
Un'altra particolaritÓ dell'anello Ŕ che tagliandolo a metÓ parallelamente al bordo si ottiene un altro nastro stavolta orientabile, con due bordi e due superfici diverse; Ŕ diventato quindi orientabile. La cosa interessante Ŕ che i due bordi separati dalla forbice rimangono un solo bordo, quindi la figura viene completamente tagliata a metÓ, ma rimane attaccata; tagliando ancora a metÓ il secondo si ottengono due nastri con torsione intera uno dentro l'altro. Se invece tagliamo l'anello a un terzo della sua larghezza si possono fare due giri con la forbice e si ottengono due nastri concatenati, uno grande la metÓ dell'altro, dove quello piccolo Ŕ ancora un nastro di M÷bius, con mezza torsione, mentre quello grande ha una torsione intera.
Teoria dei grafi e teorema dei colori
Affrontiamo il problema dei colori su un anello di M÷bius considerando la teoria dei grafi. In generale questa formulazione prevede che i vertici di ciascun grafo planare possano essere colorati utilizzando al massimo quattro colori, in modo tale che due vertici adiacenti non ricevano mai lo stesso colore. Questa rappresentazione associa ogni regione della mappa a un vertice del grafo: due vertici sono connessi da uno spigolo se e solo se le due regioni corrispondenti hanno un segmento di bordo in comune.
Spostiamo ora il problema della colorazione su una superficie chiusa piuttosto che su un piano, e grazie alla congettura di Heawood sappiamo che il massimo numero di colori necessari dipende dalla caratteristica di Eulero (X) della superficie, in accordo con la formula:

L'anello di M÷bius ha caratteristica di Eulero pari a 0, dunque la p risultante sarebbe 7. Dato per˛ che si tratta di una superficie non orientata, a questo valore dobbiamo sottrarre 1 e otterremo cosý che il numero minimo di colori Ŕ pari a 6.
Numero cromatico
Ribaltando la prospettiva che abbiamo seguito finora, definiamo numero cromatico di una superficie l'indicazione del numero massimo di regioni che possono essere tracciate su di essa in modo che a ogni regione venga attribuito un colore differente e che ogni colore confini con tutti gli altri. Sappiamo che quello dell'anello di M÷bius Ŕ pari a 6, dunque vediamo una possibile mappatura:

Notare che l'estremitÓ destra e sinistra si congiungono con una rotazione di 180% (dunque la regione fucsia si congiunge), e che i calori devono essere gli stessi su entrambe le facce del foglio di partenza.
Concludiamo dicendo che sei colori sono necessari per avere la garanzia che nessuna regione di una qualsiasi mappa abbia lo stesso colore di una confinante, ma questo non vuol dire che ogni mappa lo richieda per forza. Ecco ad esempio una mappatura su anello di M÷bius che usa cinque colori:

