Algoritmi e strutture dati - Alberi binari e Red-Black

Torna alla pagina di Algoritmi e strutture dati

---

 :: Algoritmi e strutture dati - Alberi binari e Red-Black ::

Alberi binari di ricerca

Gli alberi binari di ricerca sono strutture dati che possono eseguire molte operazioni su insiemi dinamici come: SEARCH, MINIMUM, MAXIMUM, PREDECESSOR, SUCCESSOR, INSERT, DELETE.
Possono essere utilizzati sia come dizionario, sia come coda di priorità.
Il tempo per le operazioni di base è proporzionale all'altezza dell'albero.

In un albero binario ogni nodo può avere al più due figli e viene rappresentato da record.

Un albero binario di ricerca viene rappresentato da una struttura dati concatenata in cui ogni nodo è un oggetto.
In un albero binario di ricerca ogni nodo contiene i seguenti campi:

• key;
• dati satellite;
• left;
• right;
• p.

Se manca un figlio o il padre i rispettivi campi assumono il valore NIL.
La radice è l'unico nodo ad avere p = NIL.

In questi alberi la memorizzazione delle chiavi deve soddisfare le proprietà degli alberi binari di ricerca:

• tutti i valori dei nodi del sottoalbero sinistro sono minori della radice;
• tutti i valori dei nodi del sottoalbero destro sono maggiori della radice.

Questa proprietà permette di visualizzare ordinatamente tutte le chiavi di un albero binario di ricerca con un semplice algoritmo di ricorsione di attraversamento simmetrico di un albero (inorder). Questo algoritmo permette di visualizzare la radice fra i valori del suo sottoalbero sinistro e destro.

L'algoritmo di attraversamento anticipato di un albero (preorder) invece permette di visualizzare la radice prima dei valori dei suoi sottoalberi.

L'algoritmo di attraversamento posticipato di un albero (postordine) visualizza la radice dopo i valori dei suoi sottoalberi.

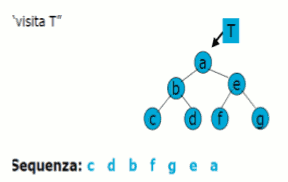
La procedura INORDER – TREE - WALK (ROOT [T]) stampa i nodi in ordine nel tempo O(n) con n nodi. La procedura TREE – SEARCH dato un puntatore alla radice e una chiave k, restituisce un puntatore a un nodo con chiave k se esiste, altrimenti restituisce il valore NIL. Tempo O(h).
Con la procedura TREE – MINIMUM si seguono i puntatori left dei figli a sinistra, fino a quando viene incontrato NIL. Restituisce un puntatore all'elemento minimo del sottoalbero con radice in un nodo x.
TREE – MAXIMUM equivale al TREE – MINIMUM. Tempo O(h).
TREE – SUCCESSOR: il successore di un nodo x è il nodo con la più piccola chiave che è maggiore di key[x]. Restituisce il successore di un nodo x in un albero binario di ricerca, se esiste, o NIL se x ha la chiave massima nell'albero. TREE – PREDECESSOR è analogo. Tempo O(h).
La TREE – INSERT riceve un nodo z per il quale key[z] = v, left[z] = NIL e right[z] = NIL; modifica l'albero di ricerca T e qualche campo di z in modo che z sia inserito in una posizione appropriata nell'albero.
Inizia dalla radice dell'albero e segue un percorso verso il basso. Tempo O(h).
La TREE – DELETE richiede come argomento un puntatore al nodo z da cancellare.
Se:

• z non ha figli, il padre p[z] viene modificato per sostituire z con NIL come suo figlio;
• z ha un figlio solo, tolgo z creando un nuovo collegamento tra suo figlio e suo padre;
• z ha due figli, si crea un nuovo collegamento per rimuovere il suo successore y che non ha un figlio sinistro, poi si sostituisce la chiave e i dati satelliti di z con la chiave e i dati satelliti di y.

Tempo O(h).

Alberi Red-Black

Gli alberi di ricerca Rosso–Neri sono alberi binari che utilizzano un bit in più di memoria per ogni nodo per identificare il nodo ovvero il colore associato a quel determinato nodo: Rosso o Nero.
Questi alberi sono approssimativamente bilanciati: assegnando vincoli al modo in cui possono essere colorati i nodi, garantisce che nessun percorso sia più di due volte più lungo di qualsiasi altro.
Ogni nodo contiene i seguenti campi:

• parent: puntatore al genitore;
• left, right: puntatore ai figli;
• color: colore del nodo;
• key, data: chiave e dati.

Un albero di ricerca per essere Rosso – Nero deve soddisfare le seguenti proprietà:

1. il nodo radice è sempre NERO;
2. i valori NIL sono NERI;
3. se un nodo padre è rosso, allora entrambi i suoi figli devono essere ROSSI;
4. per ogni nodo, tutti i percorsi da quel nodo fino alle foglie discendenti contengono lo stesso numero di nodi neri.

I nodi NIL vengono rappresentati da una sola sentinella che semplifica gli alberi rosso – neri. Questo nodo sentinella evita di trattare diversamente i puntatori ai nodi dai puntatori nil. Al posto di un puntatore nil, si usa un puntatore ad un nodo nil.

Definiamo altezza nera di un nodo x, indicata da bh(x), il numero di nodi neri lungo un percorso che inizia dal nodo x (ma non lo include) e finisce in una foglia. Per la proprietà 4, tutti i percorsi da un nodo hanno lo stesso numero di nodi neri.
Per definizione: l'altezza nera di un albero è l'altezza nera della sua radice.
Tutte le operazioni effettuate (ricerca, massimo, minimo, precedente e successivo) su di un albero Rosso-Nero, hanno una complessità pari all'altezza dell'albero stesso ovvero h = O(log n).
Le operazioni di inserimento e cancellazione anche anch'essa questa complessità però dato che modificano l'albero potrebbero violare le proprietà degli alberi Rosso-Neri con la necessità quindi di ripristinare queste proprietà.
Per ripristinare queste proprietà occorre modificare il colore di alcuni nodi e modificare la struttura dei puntatori. Per modificare la struttura dei puntatori occorre fare delle rotazioni verso destra o sinistra.

ROTAZIONI PER L'INSERIMENTO O(log n)

Caso 1: lo zio y di z è rosso.
Caso 2: lo zio di z è nero e z è un figlio destro.
Caso 3: lo zio di z è nero e z è un figlio sinistro.

ROTAZIONI PER LA CANCELLAZIONE O(log n)

La procedura RB – DELETE rimuove un nodo e successivamente chiama la RB – DELETE – FIXUP che cambia i colori e fa delle rotazioni per ripristinare le proprietà red – black.

Se il nodo y rimosso è nero:

• se y era la radice e un figlio rosso di y diventa la nuova radice si viola la proprietà 1;
• se x e p[y] (ora anche p[x]) erano rossi, allora si viola la proprietà 3;
• se qualsiasi percorso che conteneva y ha un nodo nero in meno, la proprietà 4 è violata da qualsiasi antenato di y. Si corregge dicendo che x ha un nodo nero extra.

L'obbiettivo è di spostare il nero extra in alto nell'albero finchè:

• x punta a un nodo rosso e nero e di allora coloro di nero x;
• x punta alla radice e allora il nero extra può essere rimosso;
• vengono fatte rotazioni e ricolorazioni.

Caso 1: il fratello w di x è rosso
Dato che w deve avere figli neri possiamo cambiare i colori di w e p[x] e fare una rotazione sinistra di p[x]. Il nuovo fratello di x, adesso è nero, quindi si trasforma il caso 1 nel caso 2, 3 o 4.

Caso 2: il fratello w di x è nero ed entrambi i figli di w sono neri
Dato che anche w è nero, tolgo un nero sia da x che da w, lasciando x con un solo nero e w rosso. Poi aggiungo un nero extra a p[x] per compensare la mancanza del nero. Il nuovo nodo x viene colorato di nero.

Caso 3: il fratello w di x è nero, il figlio sinistro di w è rosso e il figlio destro di w è nero
Possiamo scambiare i colori di w e di suo figlio sinistro left[w] e poi effettuare una rotazione destra di w. Il nuovo fratello w di x ora è nero con un figlio destro rosso, quindi abbiamo trasformato il caso 3 nel caso 4.

Caso 4: il fratello w di x è nero e il figlio destro di w è rosso
Si cambia qualche colore e si fa una rotazione sinistra di p[x], si rimuove il nero extra da x rendendolo singolarmente nero.

---

Torna alla pagina di Algoritmi e strutture dati