:: Affidabilità statistica ::
Dal momento in cui mettiamo in funzione un componente noi non possiamo sapere l'esatto momento in cui esso si guasterà.
Si definisce l'affidabilità empirica come: RN(t) = ns(t) / n → dove ns indica il numero di componenti che all'istante t non si sono ancora guastati, mentre n corrisponde al numero totale di componenti.
Dall'affidabilità empirica si può ricavare anche l'inaffidabilità empirica: FN=1-RN = ng(t) / n
L'andamento dei guasti suggerisce un istogramma sperimentale delle frequenze relative dove ∆t indica l'intervallo di tempo tra un rilievo ed il successivo, tale larghezza è rappresenta da: fn(t) = FN(ti + ∆ti) – FN(ti) / n * ∆ti
Definiamo il guasto empirico come:
Così come ci siamo calcolati il valore empirico dell'affidabilità, è possibile calcolare anche il valore teorica del tempo medio al guasto MTTF (Mean Time To Failure). Tale valore è dato da:
Il secondo valore empirico altro non è che il tempo medio al guasto del sistema
I modelli del tasso di guasto
Il modello più diffuso è quello “a vasca da bagno”, il quale possiede tre zone principali caratterizzate da andamenti differenti:
- Mortalità infantile: zona che possiede un elevato tasso di guasto, la quale decresce rapidamente. Tale zona costituisce la frazione debole della popolazione presa in esame, ovvero quella sezione che evidenzia un guasto durante le prime ore di funzionamento.
- Vita Utile: è la zona che possiede un tasso di guasto costante ed il cui valore è determinato soprattutto dal livello delle sollecitazioni cui è sottoposto il componente;
- Usura: è la zona in cui il tasso di guasto cresce rapidamente, tali guasti avvengono per usura del componente
Grazie a questo tipo di andamento è possibile ridefinire la Reliability come:
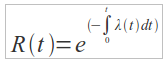
→
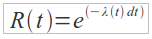
applicando dunque questa modifica anche al MTTF data prima si ottiene: 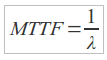
Torna alla pagina di Affidabilità Dei Sistemi?