Torna alla pagina di Informatica Teorica
:: Informatica Teorica - Complessità circuitale ::
Appunti & Dimostrazioni del 26 Maggio
Una funzione booleana f con n ingressi ed m uscite è una funzione che associa ad ogni stringa binaria di lunghezza n una stringa binaria di lunghezza m, ovvero:
f: {0,1}n -> {0,1}m
Data una funzione f che appartiene alla classe Bn (con n numero di variabili), il numero di stringhe che può avere in ingresso è 2n, mentre le diverse funzioni booleane ottenibili sono 2 elevato alla 2n.
Consideriamo ad esempio una B1:
| x | f1 | f2 | f3 | f4 |
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
Come ci aspettavamo, con una variabile abbiamo 21=2 stringhe in ingresso, e 22=4 funzioni in uscita. In particolare, per quanto riguarda queste ultime:
Consideriamo come secondo esempio una B2, per la quale ci aspetteremo di avere 22=4 possibili stringhe in ingresso, e 24=16 funzioni in uscita.
| x1 | x2 | f1 | ... | f16 |
| 0 | 0 | 0 | ... | 1 |
| 0 | 1 | 0 | ... | 1 |
| 1 | 0 | 0 | ... | 1 |
| 1 | 1 | 0 | ... | 1 |
Per rapidità non sono stati riportati in tabella tutti i valori delle funzioni intermedie, ma è importante sottolineare che ognuna di esse è ottenibile dalla combinazione dei connettivi logici applicati alle due variabili. L'insieme dei connettivi che permettono di esprimere tutte le funzioni booleane di una classe Bn sono chiamati base per Bn, la più utilizzata delle quali è la base canonica, composta dagli operatori AND, OR e NOT.
I circuiti booleani sono un modello di calcolo diverso rispetto a quello delle MdT, e rappresentano la controparte teorica dei circuiti digitali.
Un circuito booleano è un grafo diretto e aciclico, i cui nodi sono etichettati. Distinguiamo:
Altri due concetti importanti sono quelli di:
Un circuito booleano C con n nodi di ingresso ed m nodi di uscita calcola la funzione f:{0,1}n->{0,1}m se, per ogni assegnamento di valori alle n variabili che etichettano i nodi di ingresso, il valore calcolato da C è uguale a f(x1,x2,...,xn).
Una volta codificati opportunamente i linguaggi in binario, il nostro obiettivo è quello di usare i circuiti booleani per verificarli. Ma i circuiti hanno un numero fisso di ingressi, mentre i linguaggi possono contenere stringhe di lunghezze diverse, quindi che si fa? Semplice: invece di usare un unico circuito per verificare l'appartenenza a un linguaggio ne useremo un'intera famiglia!
Una famiglia di circuiti C è una lista infinita di circuiti, (C0, C1, C2, ...), dove Cn ha n variabili di ingresso. Diciamo che C decide un linguaggio A su {0,1} se, per ogni stringa w, w appartiene ad A se e solo se Cn(w)=1, dove n in questo caso è la lunghezza di w.
Per arrivare a definire la size-complexity di un circuito dobbiamo prima introdurre un po' di concetti:
Abbiamo tutto quello che ci serve per affermare che:
La size-complexity circuitale di un linguaggio è la size-complexity della famiglia minimale di circuiti per quel linguaggio.
Stesso discorso: arriveremo alla definizione della depth-complexity di un circuito solo dopo aver introdotto alcuni concetti basilari:
Abbiamo tutto quello che ci serve per affermare che:
La depth-complexity circuitale di un linguaggio è la depth-complexity della famiglia minimale di circuiti per quel linguaggio.
Esiste una relazione tra la complessità circuitale e la tempo-complessità di un linguaggio. Intuitivamente siamo infatti portati a pensare che ogni linguaggio con ridotta complessità nel tempo abbia anche una piccola complessità circuitale. Per chi però non si fidasse del proprio intuito, eccoci servito il Teorema 1:
Sia t:N->N una funzione con t(n)>=n. Se A appartiente a TIME(t(n)), allora A ha una complessità circuitale pari a O(t2(n)).
La dimostrazione non è richiesta, ma è importante ricordare che oltre al teorema in sé prova anche che un circuito booleano può essere simulato da una MdT.
Così come per le formule booleane, anche i circuiti booleani possono essere o meno soddisfacibili; in particolare, lo sono quando una certa configurazione di valori passati agli ingressi fa sì che l'uscita del circuito sia pari a 1.
Il problema CIRCUIT-SAT si occupa di verificare se un circuito è soddisfacibile, o più formalmente:CIRCUIT-SAT = {<C> | C è un circuito booleano soddisfacibile}
Vediamo ora il teorema:
CIRCUIT-SAT è NP-completo.
Ricordiamo che i 3CNF-formula sono formule in forma normale congiuntiva con clausole composte da 3 letterali, e che una 3SAT è una 3CNF-formula soddisfacibile. Il teorema:
3SAT è NP-completo.
Dimostrazione
Che 3SAT fosse NP-completo l'avevamo già dimostrato col teorema di Cook-Levin nel capitolo sulla NP-Completezza, ma volete mettere ridimostrarlo con i circuiti booleani?
Come sappiamo, un linguaggio B è NP-completo se soddisfa due condizioni:
La prima condizione è verificata grazie alla dimostrazione del Teorema 1, in cui si mostrava possibile l'utilizzo di una MdT n.d. per simulare un circuito.
Per la seconda condizione proveremo a ridurre il problema CIRCUIT-SAT a quello 3SAT in tempo polinomiale. Si parla perciò di una riduzione da un circuito C a una formula Φ, tale che C è soddisfacibile se e solo se Φ lo è.
Le variabili di un circuito sono gli ingressi x1,...,xl e le porte g1,...,gm, che dovranno essere rimappate nelle variabili di Φ etichettate come w1,...,wl+m.
Passiamo ora a costruire le clausole, che dovranno descrivere i tre operatori logici della forma canonica (AND, OR, NOT). Per semplicità utilizzeremo anche l'operatore implica, per il quale vale la proprietà:(P->Q) = (~P v Q)
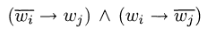
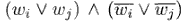
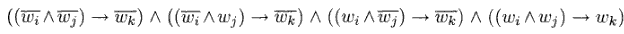
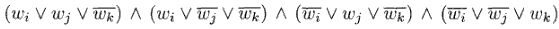
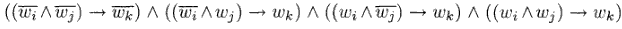
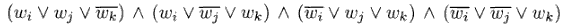
A queste clausole ne aggiungiamo un'altra: (wm), che rappresenta il nodo di uscita del circuito C.
Quello che resta da fare è riscrivere le clausole in forma 3SAT (tre letterali per clausola). Dato che le uniche clausole a non essere in 3SAT (quelle del NOT e quella di uscita) hanno meno di 3 letterali, basterà semplicemente replicare un letterale quante volte serve per arrivare a 3, e metterlo in OR con gli altri. Ad esempio (wm) diventa:
(wm v wm v wm)
Ora che sappiamo come convertire variabili e porte logiche di un circuito in una formula 3SAT equivalente, possiamo affermare che se CIRCUIT-SAT è NP-completo (Teorema 2) allora anche 3SAT lo è, perché la riduzione da uno all'altro è tempo polinomiale nella dimensione del circuito iniziale.