Torna alla pagina di Informatica Teorica
:: Informatica Teorica - NP-Completezza ::
Appunti & Dimostrazioni del 12 Maggio
Se A ≤P B e B ∈ P, allora A ∈ P
Dimostrazione
Capiamo bene le due ipotesi:
La tesi del teorema ci dice che date le premesse A si troverà in P, ovvero avrà una MdT deterministica N che lo deciderà in tempo polinomiale. Scriviamola:
N = "su ingresso w:
Dato che f è una riduzione da A a B, w ∈ A se e solo se f(w) ∈ B, e quindi M accetterà f(w) se e solo se w è accettata da A. Ottenuto quello che volevamo, dobbiamo verificare che N sia risolvibile in tempo polinomiale, e lo è perché sia l'operazione di riduzione che l'esecuzione di M lo sono. La tesi è dunque verificata!
I 3cnf-formula sono formule in forma normale congiuntiva con clausole composte da 3 letterali. Una 3SAT è una 3cnf-formula soddisfacibile.
Veniamo al teorema:
3SAT è tempo polinomiale riducibile a CLIQUE.
Dimostrazione
Abbiamo davanti una formula booleana che deve essere riducibile in tempo polinomiale a una CLIQUE (un sottoinsieme di nodi di un grafo tutti connessi tra loro). Dovremo quindi convertire la 3SAT in un grafo che contenga una CLIQUE se e solo se la 3SAT è soddisfacibile.
Come costruiamo il grafo? Teniamo conto che partiamo da una formula di questo tipo:
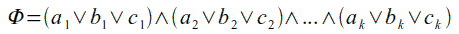
e che vogliamo una funzione che ci generi una stringa di tipo <G,k> (dove G è il grafo e k il numero di nodi che compongono la cricca).
Come prima cosa stabiliamo che k corrisponda al numero di clausole di cui è composta Φ, e che organizzeremo i nodi del grafo in k gruppi da 3 nodi ciascuno.
Consideriamo la seguente 3SAT di esempio:
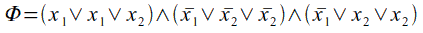
Organizziamo i nodi in k=3 gruppi da tre:
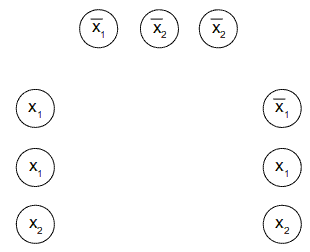
Consideriamo infine ogni coppia di nodi e li colleghiamo con un arco solo se rispettano entrambe le regole:
Tornando al nostro esempio, mostriamo come devono essere i collegamenti del primo nodo del gruppo in alto:
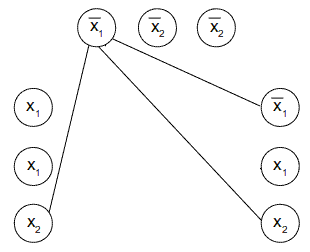
E così via.
A questo punto bisogna dimostrare che il grafo così formato abbia una k-CLIQUE se e solo se Φ è soddisfacibile. E' un "se e solo se", quindi dovremo dimostrare entrambi i sensi dell'implicazione:
(I) Φ è soddisfacibile -> k-CLIQUE
Selezioniamo da ogni clausola di Φ un letterale che sia pari a 1 (se ce ne sono diversi ne scelgo uno a caso). Dimostriamo ora (con un verificatore amichevole e alla buona) che i nodi selezionati formano effettivamente una k-CLIQUE:
V = "
(II) k-CLIQUE -> Φ è soddisfacibile
Si dimostra in modo complementare a (I): se assegniamo valore 1 ai nodi che formano la CLIQUE, per costruzione ce ne sarà almeno uno per clausola. Essendo la Φ una 3cnf-formula, se ha almeno un letterale uguale a 1 per clausola, allora sarà vera, quindi soddisfacibile.
Un linguaggio B è NP-Completo se soddisfa due condizioni:
Se B è NP-Completo e B ≤P C per C in NP, allora C è NP-Completo.
Dimostrazione
Per dimostrare il teorema dovremo verificare che siano vere entrambe le condizioni perché un linguaggio sia NP-Completo:
La tesi è perciò dimostrata.
SAT è NP-Completo.
Dimostrazione
Per dimostrare che SAT è NP-Completo dobbiamo verificare se sono soddisfatte le solite due condizioni:
Per verificare la seconda condizione bisogna costruire una riduzione tempo polinomiale per ogni linguaggio A in NP che riconduca a SAT. Cominciamo col definire una MdT non deterministica N che decide A in un tempo polinomiale, ovvero N -> nk. Introduciamo ora il cosiddetto tableau, una magnifica tabella in cui ad ogni riga corrisponde una configurazione della nostra macchina N. Le dimensioni del tableau sono nk x nk, ed è così costruito:
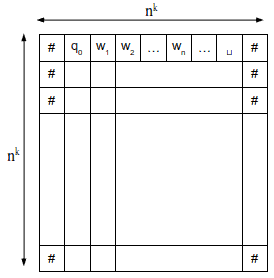
Dove:
Il tableau è detto accettante se una qualsiasi delle sue righe corrisponde a una configurazione accettante (contiene ovvero una qaccept). Quello che vogliamo fare è associare al tableau una formula che sarà soddisfatta se e solo se il tableau è accettante, perché significherebbe che A accetta w.
Introduciamo ora le variabili della nostra formula, che sarebbero poi tutti i possibili simboli che compariranno nel tableau. Prima di tutto definiamo l'alfabeto:
C = Q U Γ U {#}
, dove Q sono gli stati della macchina, Γ sono i simboli che possono essere sul nastro, e infine c'è il simbolo #.
Ad ogni cella sarà associata una variabile binaria xi,j,s, dove i e j sono le coordinate nel tableau, mentre s è un simbolo preso da C. In particolare, xi,j,s varrà 1 se in (i,j) c'è il simbolo s, 0 altrimenti.
Abbiamo tutto quello che ci serve per realizzare una Φ che corrisponda a un tableau accettante:
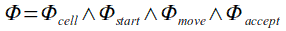
Analizziamo una per una le quattro parti in AND di cui è composta.
Φcell
Stabilisce che in ogni cella deve esserci un solo simbolo. Vediamola in formula:
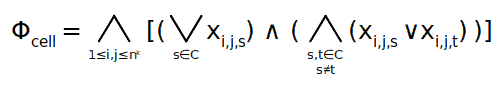
, dove il primo OR dice che all'interno di ogni cella deve esserci almeno un simbolo (e infatti richiede che almeno una delle variabili sia pari a 1), mentre il secondo AND dice che in ogni cella del tableau non deve esserci più di un simbolo, e le due parti sono in AND tra loro perché devono essere ovviamente vere entrambe.
Φstart
Stabilisce che la prima riga deve corrispondere alla configurazione di partenza della MdT N. Vediamola in formula:
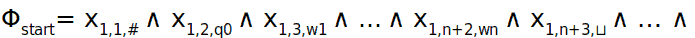
Φaccept
Garantisce che nel tableau ci sia almeno una configurazione accettante, ovvero che ci sia una qaccept. Vediamola in formula:

Φmove
Garantisce che ogni configurazione segua la precedente in modo legale, rispettando cioè la funzione di transizione di N. Per verificarla si ritagliano nel tableau delle finestre di dimensioni 2x3, e si dimostra che sono legali. Se tutte le finestre sono legali, allora è garantito che ogni configurazione del tableau segue in maniera corretta la precedente.
Facciamo un po' di esempi. Abbiamo due funzioni di transizione:
{(q1, b, R)}
{(q2, c, L), (q2, a, R)}
Consideriamo le seguenti possibili finestre:
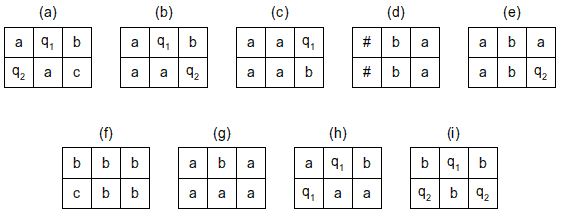
Sono legali o no?
Ora che abbiamo un'idea su come funziona la verifica della legalità delle finestre, vediamo come esprimere Φmove in formula:
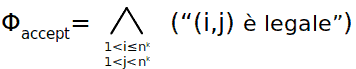
Ricapitolando, avevamo detto che:
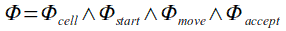
e quindi la Φ sarà soddisfatta se tutte le sue componenti saranno pari a 1. Ma dato che per costruzione abbiamo fatto sì che questa proprietà fosse vera, avremo che la Φ è soddisfacibile. Siamo dunque riusciti a trovare una formula per cui ogni A in NP è riducibile a SAT, quindi non rimane altro da dimostrare che questo avviene in tempo polinomiale.
Analizziamo le varie parti dell'algoritmo:
Il termine dominante è n2k, quindi l'algoritmo ha complessità O(n2k), che è tempo polinomiale. Fantastico: abbiamo dimostrato anche la seconda condizione per cui SAT è NP-Completo! Ora possiamo raccogliere le braccia da terra.
3SAT è NP-Completo.
Dimostrazione
Per dimostrare che 3SAT è NP-Completo dobbiamo verificare se sono soddisfatte le solite due condizioni:
Quello che dobbiamo fare è modificare la dimostrazione del SAT in modo che produca una formula nella forma normale congiuntiva con tre letterali per clausola (una 3SAT, appunto). Rivediamo la Φ di SAT:
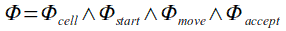
Come prima cosa verifichiamo che ogni parte sia in forma normale congiuntiva (FNC):
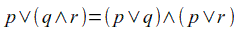
Ora che abbiamo tutte le parti della Φ in forma normale congiuntiva non ci resta che vincolare ogni clausola ad avere al massimo 3 letterali. Studiamo i vari casi possibili e le contromisure da adottare:
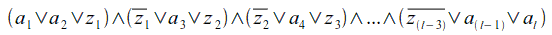
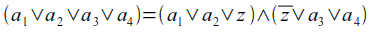
Dopo tutte queste modifiche, è più che semplice verificare che la nuova Φ ottenuta è soddisfacibile se e solo se la Φ originale lo è. Quindi, essendo la dimostrazione usata per il teorema di Cook-Levin più che valida anche per questo suo corollario, possiamo affermare che anche 3SAT è NP-Completo.