:: LPS - Macchine a stati finiti ::
Si tratta di uno strumento formale ed operazionale di modellizzazione. Questi termini hanno un preciso significato: operazionale è contrapposto a dichiarativo, mentre formale è opposto sia a informale che a semiformale. Vediamo un po'.
Ecco qual'è la differenza:
Per esempio, una definizione operazionale di un cerchio è "insieme dei punti equidistanti da un centro". La definizione dichiarativa è invece "insieme dei punti tali che XO = c, dove X sono le coordinate del punto e O quelle del centro".
Una FSM può essere rappresentata in modo equivalente da una notazione formale, oppure da un grafo opportunamente disegnato. I nodi equivalgono agli stati del sistema, mentre gli archi sono le transizioni di stato, e le etichette degli archi sono le modalità di transizione.
Di base, le FSM ricevono input. Se producono output, sono dette macchine di Mealy o Moore, di scarabottoliana memoria. Si possono usare per modellare tanta roba, ma hanno anche dei limiti: ad esempio, non sono in grado di modellare requisiti basati sul tempo o sulle performance, e non si possono comporre. Tutto questo sarà più chiaro in seguito.
Una FSM è una tripla (S, I , δ), dove:
Come dicevo sopra, la notazione grafica e quella matematica sono equivalenti. Il grafo è un grafo orientato, perché gli archi hanno una direzione.
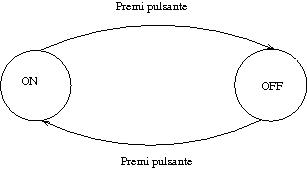
Le etichette degli archi, nel grafo, rappresentano gli input.
Per quanto riguarda δ, va notato che queste due scritture sono equivalenti:
δ(s1, i) = s2 = δ(s1, i, s2)
Ed ecco un esempio di una FSM in cui l'"orientatezza" del grafo si nota di più:
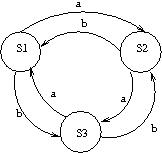
Una macchina di Mealy è una FSM che, per ciascuna transazione, produce un output. Una macchina di Moore invece è una FSM che produce output per ciascuno stato. Vediamo di tuplizzare anche codeste robe:
Macchina di Moore = tupla (S, I, O, δ, λ, F), dove
Macchina di Mealy = tupla (S, I, O, δ, λ), dove
Di solito nelle macchine di Mealy si indica anche lo stato iniziale s0, appartenente ad S.
I diagrammi che rappresentano le macchine di Mealy hanno gli archi etichettati da i/o, dove i è l'evento di input, e o è l'evento di output. Gli eventi di output possono anche essere azioni che la macchina compie.
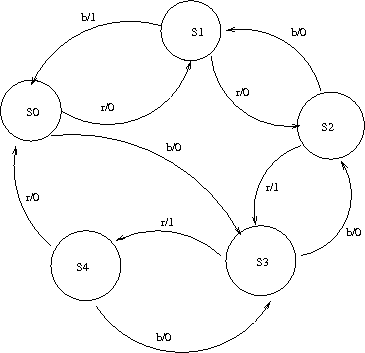
È inoltre comodo vedere una FSM di Mealy come una tupla (S, I, O, T), dove, oltre alle solite cose, ho T che è l'insieme delle transizioni.
Le transizioni sono, a loro volta, una tupla (s, i, o, s'):
D'ora in poi noi useremo FSM di Mealy, e le chiameremo solo FSM, con buona pace di Mealy.
Si può solo rappresentare un numero finito di stati: i pallogrammi infiniti non sono pratici. Per questo motivo, non è modellabile il tempo continuo come input: essendo continuo, non discreto, ed infinito, dovrei avere uno stato per ogni infinitesimo istante.
L'altro limite è che non sono composizionali. Vuol dire che quando metto insieme due macchine, una con un numero n di stati, e l'altra con m stati, avrò una FSM con n*m stati, e non n+m come potrei supporre.
Questo limite viene a galla quando si cerca di modellare tramite FSM dei sistemi distribuiti o a componenti, in cui ogni componente va per la sua strada, e comunica con gli altri componenti. Dovrei avere uno stato per ogni associazione di stati di un componente con ognuno degli stati dell'altro componente, e così via.
Ho un Produttore, un Consumatore ed un Magazzino con capienza di 2 unità.
Il Produttore ha due stati: va dall'uno all'altro prima producendo qualcosa, e poi depositandolo nel magazzino.
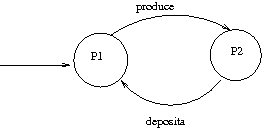
Il Consumatore ha due stati: va dall'uno all'altro prima prendendo qualcosa dal magazzino, e poi utilizzandolo.
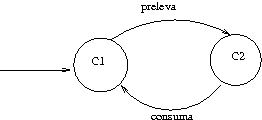
Il Magazzino ha tre stati, se lo immaginiamo con capienza di 2 oggetti. C'è lo stato in cui è vuoto, quello in cui ha 1 oggetto, e quello in cui ne ha 2, e relative transazioni legate al fatto che il Produttore deposita e il Consumatore preleva.
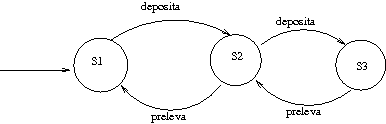
Orbene: se volessi comporre queste FSM, quanti stati ottengo? Forse 2 + 2 + 3 = 7? No: in realtà ne ottengo 12 = 2 * 2 * 3. Infatti, devo avere queste combinazioni
etc. etc. Uno stato rappresenta uno stato della macchina: se la macchina ha tanti componenti, allora ho tanti stati, che rappresentano tutte le combinazioni di modi in cui i componenti possono trovarsi tra di loro.
Per oltrepassare questo limite, occorrono altre macchine, che vedremo poi, dette macchine di comunicazione.
Adesso segue una bella lista di proprietà relative alle FSM
Due stati di una FSM sono equivalenti se, per ogni sequenza di input, le sequenze di output provenienti dai due stati sono le stesse.
Vuol dire che devo avere due transizioni così:
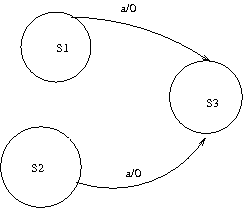
Se 2 stati non sono equivalenti, allora sono distinguibili. Se una macchina non ha coppie di stati equivalenti, è detta minimizzata o ridotta. Ci sono degli algoritmi che individuano le coppie di stati equivalenti e li fanno collassare in un unico stato.
Inoltre, se due macchine hanno gli stati "accoppiabili", sono equivalenti. Per essere precisi, se ho una macchina M1 ed una M2, per essere equivalenti:
Se 2 macchine non sono equivalenti, sono distinguibili.
2 stati sono k-equivalenti se, per ogni sequenza di input di lunghezza k, le sequenze di output dei 2 stati sono le stesse. Si può anche definire la k-distinguibilità allo stesso modo, ed estendere la definizione alle macchine k-equivalenti.
La sequenza di input la si deve vedere così: parto da uno stato e applico quella sequenza di input. Ogni passo di questa sequenza attiverà una transizione che mi porterà o nello stesso stato, o in altri stati etc e produrrà un certo output. Se la stessa sequenza, fatta a partire da un altro stato, mi produce lo stesso output, allora i due stati sono k-equivalenti, con k che è la lunghezza di tale sequenza di input.
Una FSM è completamente specificata se, per ogni stato e per ogni input, c'è una transizione che comprende questa accoppiata. Ciò vuol dire che, se ho 3 stati e 4 input, tutti e tre gli stati devono saper gestire i 4 input diversi, per poter definire la macchina come completamente specificata.
In generale, però, le macchine con cui abbiamo a che fare NON sono completamente specificate. La cosa è anche intuitiva: è un po' inutile specificare che cosa succede quando premo l'acceleratore elettronico di un'automobile spenta, per intenderci.
Ci sono anche dei sistemi per ottenere una macchina completamente specificata a partire da una macchina non completamente specificata.
Aggiungo agli stati dei loop, con output null oppure '''error',, in corrispondenza con gli input precedentemente non gestiti.
Ad esempio, se dei 3 input un certo stato ne gestisce solo 2, il terzo lo metto in una transizione di loop e ne etichetto l'output come null oppure '''errore'.
Questo è veramente balordo. Ad uno stato a cui manchi la gestione di qualche input, devo aggiungere tante transizioni quanti sono (input)x(output)x(stati)!
Per capire la follia di questo sistema, se ho 3 stati, 4 input e 2 output, e il mio stato (il numero 1) gestisce solo 2 input, devo aggiungere una transazione che porta ad ogni stato (anche transazioni di loop) mancante per ogni input, per ogni output: mi mancano 2 input, ho 3 stati e 2 output => 2 * 3 *2 = 12 transazioni.
Un'assurdità.
Semplicemente, scrivo da qualche parte che "non si può applicare questi input allo stato si"...
Una FSM è deterministica se, dato uno stato ed un input, il passo che può fare è determinato. Questo significa che, se ho un certo input che arriva in uno stato, il passo successivo è solo 1. Se ne ho 2 diversi, allora non è deterministica, perché non saprei determinare con esattezza quale passo fare. Deve esserci quindi una sola uscita per ogni input.
Una FSM è fortemente connessa se, per ogni coppia di stati, c'è una sequenza di input che li congiunge.
La sequenza di input, come dicevamo prima per la k-equivalenza, viene applicata a partire dal primo stato. Questo stato reagirà in modi diversi: dopo tot input saremo finiti in un certo punto.
Una FSM è inizializzata se esiste uno stato sinit segnato come stato iniziale.
ATTENZIONE LA LEZIONE 10 NON E' PIU' OGGETTO D'ESAME QUEST'ANNO
Le FSM che considereremo nei vari esercizi etc., sono da considerarsi:
Adesso vediamo alcune sequenze di input che hanno delle proprietà particolari. Queste sequenze hanno un senso in un particolare contesto, che viene indicato per ogni sequenza.
Il problema è: non so qual'è lo stato iniziale, e voglio mandare in input una sequenza di input tale che lo stato finale sia noto.
Una sequenza è una synchronizing sequence se, applicata a partire da uno qualunque degli stati, essa conduce sempre allo stesso stato finale. Da notare che non ci interessa l'output, ma solo lo stato finale.
Anche qui, non so quale sia lo stato iniziale, ma voglio conoscere lo stato finale osservando l'output.
Una sequenza di input è homing se, dopo averla applicata, siamo in grado di determinare lo stato finale osservando la sequenza degli eventi di output. Una sequenza di sincronizzazione è anche homing, ma non il contrario (synchronizing)⊂(homing)
Non so quale sia lo stato iniziale, ma, osservando l'output, voglio scoprire quale sia. Se sono in grado di farlo, applicando una certa sequenza di input, allora quella sequenza di input è detta distinguishing. Alla fine della sequenza so con certezza in quale stato ero alla partenza.
Non conosco lo stato iniziale, e voglio stabilire se un certo stato è iniziale osservando l'output.
Una sequenza è UIO se, dopo averla applicata in input, posso determinare se lo stato iniziale fosse un particolare sn oppure no; in caso negativo potrei non sapere in quale stato mi trovi.
Le macchine che abbiamo visto finora non sono in grado di modellare la memoria interna, perché sanno gestire solo input e output. La memoria non è né input né output. Pertanto, per poterla modellare occorre estendere le FSM con il concetto di variabile.
La definizione matematica di una macchina a stati finiti estesa (EFSM) è la seguente: una tupla (S, I, O, V, T), dove S, I, O sono le solite cose; V è l'insieme della variabili, e T quello delle transizioni.
Le transizioni, a loro volta, sono definite così: (s, i, o, g, a, s') dove:
Le cose nuove sono la guardia e l'assegnamento ad una variabile. L'assegnamento va beh, si capisce: se la variabile si chiama x e voglio assegnarle il valore 3, faccio x:= 3.
Per quanto riguarda la guardia, invece, si tratta di una condizione booleana che fa sì che la operazione sulla variabile sia eseguita o no. Il fatto che sia booleana ci dice che questa condizione o è verificata, o non lo è. Se è verificata, l'operazione a viene eseguita. Altrimenti, non viene eseguita. Inoltre, la guardia g è definita sulla variabile, e non su input o output.
Per fare un esempio, se scrivo una transizione così: (s1, tasto +, scrivi numero, var >= 0, a:=a + 1, s2), vuol dire che vado dallo stato s1 all's2 quando arriva l'input "tasto +", producendo l'output "scrivi numero", e che la variabile a viene incrementata di 1 solo se la variabile var è >= 0.
La guardia può anche non esserci: in questo caso, l'operazione viene eseguita sempre.
Lo stato globale è definito come una tupla (s, σ), in cui:
Essendo V l'insieme delle variabili, questa definizione vuol dire semplicemente che lo stato globale è una fotografia dello stato della macchina in un certo istante. In quell'istante, la macchina sarà in un certo stato s, e le sue variabili avranno un certo valore. La situazione in cui le variabili hanno un certo valore la definisco con la σ (sigma).
Ad esempio, se ho 3 variabili a, b e c, e la situazione è:
allora lo stato globale è (s1, σ = (a = 3, b = 2, c = 100)).
Dopo lo stato globale, c'è anche la transizione globale, che è una tupla in cui si definisce uno stato globale iniziale, uno finale, e dell'i/o in mezzo.
La def è la seguente: ((s, σ), i, o, (s',σ')), dove
Questa tupla è una transizione globale se esiste una transazione, definita come (s, i, o, g, a, s'), in cui
Nell'esempio del salvadanaio elettronico (da inserire...), una transizione ((empty, coin=0), inc, red, (not empty, coin = 1)) è una transizione globale, perché la valutazione sulle variabili σ qui specificata, cioè coin = 0, soddisfa la guarda che, nella macchina, porta dallo stato empty allo stato non empty. Idem per la σ'.
Invece, ((non emtpy, coin = 5), inc, red, (non empty, coin = 7)) non è una transizione globale, perché, se anche σ soddisfa la guardia, la σ' non la soddisfa affatto: nella mia macchina se incremento vado da 5 a 6, e non a 7.
Un grafo di raggiungibilità lo creo stabilendo che i nodi sono stati globali, e gli archi sono transazioni globali.
Quindi, avrò uno stato per ogni combinazione di stato e di memoria, e archi tante quante le combinazioni tra transizioni "normali" e stato di memoria.
In particolare, se la memoria è finita, allora anche la combinazione tra stati e memoria sarà un numero finito; idem per la combinazione tra transizioni e stati di memoria. E allora, in queste condizioni è possibile trasformare una EFSM in una FSM semplice, in cui ho tanti stati quante sono le combinazioni tra stati della EFSM e stati in cui la memoria può trovarsi in EFSM.
Se ho per esempio 3 stati, e una variabile che può assumere 5 valori, posso ipotizzare che avrò 3*5 stati:
...
Se invece la variabile ha un range infinito, allora la FSM avrebbe un numero infinito di stati, e non sarebbe più una macchina a stati finiti...
Sopra si parlave delle macchine di comunicazione come del sistema per ovviare la triste proprietà delle FSM standard quando vengono composte. Le macchine di comunicazione aggiungono al modello delle macchine il concetto di canale di comunicazione. Tramite questo canale le varie FSM possono scambiarsi messaggi per agire come un sistema unico.
Una CFSM è una coppia (C, P) dove C è un insieme di canali, e P un insieme di processi.
Il processo è una tupla (S, I, O, T):
La transizione a sua volta è una tupla che può assumere una di queste tre forme:
E adesso vediamo di fare un po' di ordine.
Il processo, come si sarà capito, è l'equivalente della singola FSM. Lo chiamo processo perché il fatto che possa comunicare con altre FSM lo rende in grado di essere eseguito indipendentemente, ma sincronizzandosi in qualche modo con le altre FSM.
Per quanto riguarda le transizioni, invece, la parte in mezzo, (quella che è null, c?i oppure c!o) ha a che fare con la capacità del processo di inviare messaggi sul canale. Il canale è indicato da c, l'azione che esegue sul canale può essere una ? o una !, e ciò che deriva da quest'azione è i oppure o. Ed ecco la spiegazione:
Quando si rappresenta una CFSM, occorre scrivere prima lo schema della CFSM intera, con i vari processi ed i canali direzionati tramite cui parlano. I canali hanno il loro nome, e questo è univoco per tutti i processi.
Poi, i singoli processi vanno scritto come le solite FSM.
Facendo un po' il mix di tutto, mi invento a questo punto le CFSM estese, in cui aggiungo ai canali la faccenda delle guardie, delle variabili e delle azioni. Le cose quindi si complicano un po'.
I processi sono definiti come tuple (S, I, O, V, T), dove V sono le variabili.
Anche le transizioni si fanno complicate, perché assumono una di queste tre forme:
Si tratta praticamente di una fusione tra le transizioni delle EFSM e quelle delle CFSM: infatti ho le guardie, le azioni sulle variabili e le azioni sul canale.
Non siamo ancora soddisfatti, e vogliamo espandere ulteriormente le CFSM estese appena viste, indicando nelle transazioni anche l'intervallo temporale in cui l'azione può avvenire.
Le transazioni assumono quindi la forma (s, g, a|i/o, s'. [t1, t2]) in cui:
Possiamo applicare anche qui il concetto di transizione globale. Una coppia ((θ, σ), (θ', σ')) è detta transazione globale se, per ogni processo P
In pratica, le θ sono gli stati dei vari processi, mentre σ mi dice come stanno i canali. La σ è triforme (che aggettivo è?), così come sono 3 le operazioni relative ai canali:
Allo stesso modo, lo stato globale è una fotografia del sistema in un certo istante di tempo, ed è composto da una bella combinazione di tutti gli stati, dei canali etc. etc.
Il grafo di raggiungibilità lo si ottiene mettendo gli stati globali come nodi, e le transizioni globali come archi. Come avevamo visto prima, posso arrivare ad ottenere una FSM di base. Ovviamente, dipende anche dalla quantità di memoria dei vari processi: processi con memoria infinita non sono rappresentabili con macchine a stati finiti.