Uni.LezECT04 History
Hide minor edits - Show changes to markup
Changed lines 5-7 from:
:: Economia ed Organizzazione Aziendale ::
Lezione 7/10/2008
to:
:: Economia del Cambiamento Tecnologico ::
Lezione 07/10/2008
Changed line 56 from:
 \\\ to:
 \\\
Changed lines 14-15 from:
to:
Deleted lines 77-96:
Esercitazione a computer
Nell'esercizio proposto da Dallara abbiamo le variabili di cui abbiamo parlato nella scorsa lezione divise per anni.
Di queste variabili noi dobbiamo rilevare:
- gli indici di posizione, tra cui
- minimo
- primo quartile
- media aritmetica
- mediana
- terzo quartile
- massimo
- gli indici di variabilità
- varianza(misura della rischiosità finanziaria)
- scarto quadratico medio (varianza)
- scarto interquartile (terzo quartile-primo)
- coefficiente di variazione (scarto quadratico medio/media artmetica)
- gli indici di forma
Changed line 71 from:
to:
Changed line 75 from:
to:
Added lines 81-98:
Nell'esercizio proposto da Dallara abbiamo le variabili di cui abbiamo parlato nella scorsa lezione divise per anni.
Di queste variabili noi dobbiamo rilevare:
- gli indici di posizione, tra cui
- minimo
- primo quartile
- media aritmetica
- mediana
- terzo quartile
- massimo
- gli indici di variabilità
- varianza(misura della rischiosità finanziaria)
- scarto quadratico medio (varianza)
- scarto interquartile (terzo quartile-primo)
- coefficiente di variazione (scarto quadratico medio/media artmetica)
- gli indici di forma
Changed lines 14-15 from:
to:
Changed lines 77-80 from:
Viene così perchè il livello di produzione è dato.
to:
Viene così perchè il livello di produzione è dato.
Esercitazione a computer
Changed lines 13-14 from:
to:
Changed lines 70-71 from:
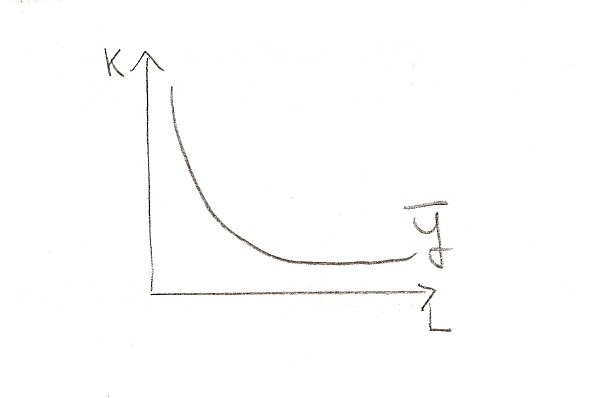
Nel caso K e L siano variabili la funzione di produzione si può rappresentare con una mappa di isoquanti
to:
Nel caso K e L siano variabili la funzione di produzione si può rappresentare con una mappa di isoquanti con una funzione così data:
δY δY
---- dL + ---- dK = 0
δL δK
 Viene così perchè il livello di produzione è dato.
Added lines 65-70:
- non sceglie di operare nel primo perchè può aumentare il prodotto totale aumentando il fattore produttivo variabile (cioè assume più personale) [siccome i rendimenti marginali del fattore variabile sono crescenti non mi conviene fermarmi ma espandere la produzione]
- non sceglie di operare nel terzo perchè è sufficiente ridurre le quantità di fattori produttivi variabili per aumentare la produzione totale(perciò deve licenziare poverino)
Insomma: nel secondo stadio sfrutta al meglio le risorse di produzione
Nel caso K e L siano variabili la funzione di produzione si può rappresentare con una mappa di isoquanti
Changed line 64 from:
+Tesi+: l'imprenditore razionale neoclassico per massimizzare il profitto opera nel secondo stadio. Perchè?
to:
Tesi: l'imprenditore razionale neoclassico per massimizzare il profitto opera nel secondo stadio. Perchè?
Changed line 64 from:
Tesi: l'imprenditore razionale neoclassico per massimizzare il profitto opera nel secondo stadio. Perchè?
to:
+Tesi+: l'imprenditore razionale neoclassico per massimizzare il profitto opera nel secondo stadio. Perchè?
Added lines 49-64:
Notazioni sull'esercizio
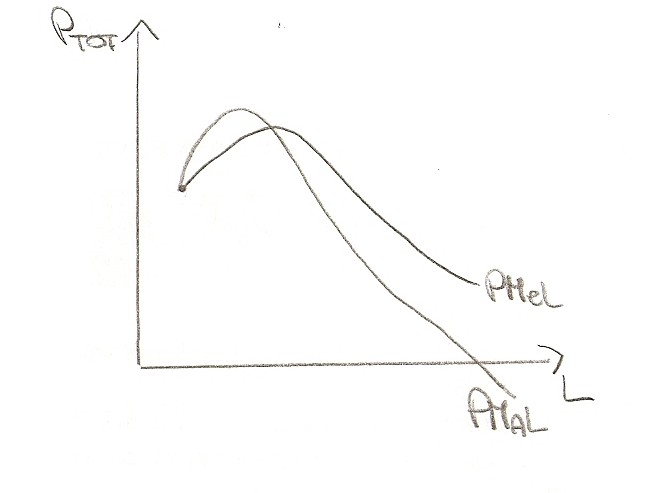
- PMaL = PMeL nel punto in cui PMeL è massimo
- PMaL = 0 nel punto in cui la funzione di produzione è massimo
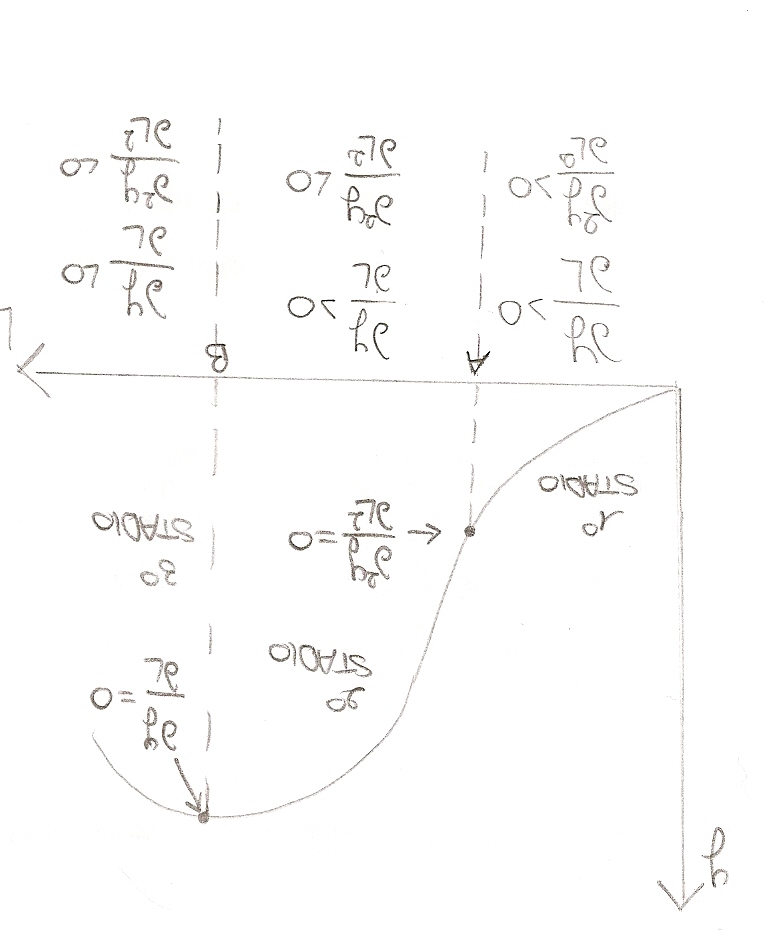
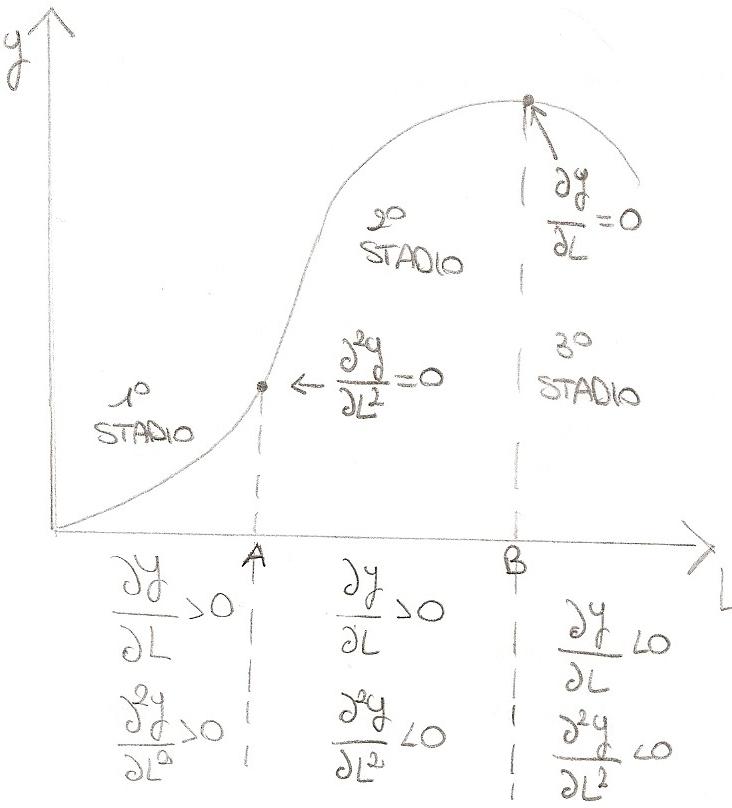
In una fase di produzione si possono individuare 3 stadi:
- 1° stadio: corrisponde all'intervallo compreso tra l'origine degli assi e il punto di intersezione tra PMeL e PMaL o il punto in cui il PMeL è massimo
- 2° stadio: corrisponde all'intervallo compreso tra il punto di massimo del PMeL e il punto in cui il PMaL si annulla (oppure il punto di massimo della funzione di produzione)
- 3° stadio: dal punto in cui il PMaL è nullo fino alla fine del piano
Tesi: l'imprenditore razionale neoclassico per massimizzare il profitto opera nel secondo stadio. Perchè?
Changed lines 42-48 from:
to:
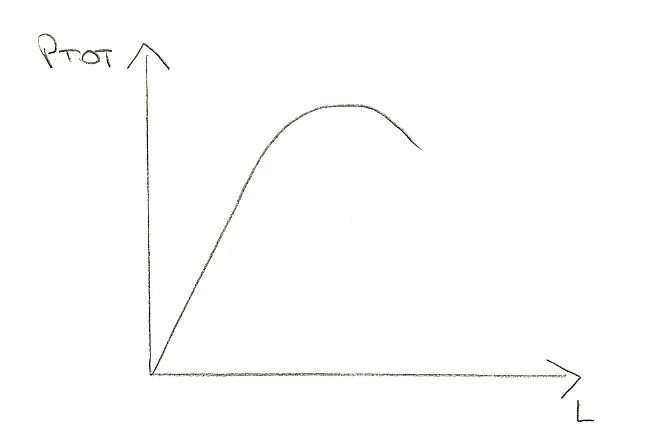
- calcolare la produttività media e marginale del fattore di produzione variabile
- costruire i grafici della produzione totale e delle produttività
- commentare i grafici individuando i punti più significativi
- (calcolare la funzione di produttività del fattore produttivo costante)
  \\
Changed line 12 from:
to:
Added lines 18-40:
Esercizio
T L Y PMeL PMaL
1 0 0 -
3
1 1 3 3
5
1 2 8 4
4
1 3 12 4
3
1 4 15 3,75
2
1 5 17 3,4
0
1 6 17 2,83
-1
1 7 16 2,29
-3
1 8 13 1,63
|