Torna alla pagina di Economia del Cambiamento Tecnologico
:: Economia del Cambiamento Tecnologico ::
Lezione 21/11/2008
In questo modello, come da titolo, si trovano due settori produttivi:
Questo modello comprende 15 equazioni. Le prime 7 sono uguali a quelle del modello precedente (leggermente modificate):
[Nota: poichè il sistema socioeconomico è articolato in 2 settori è necessario esprimere le variabili di quantità in valore monetario]
Ottava equazione
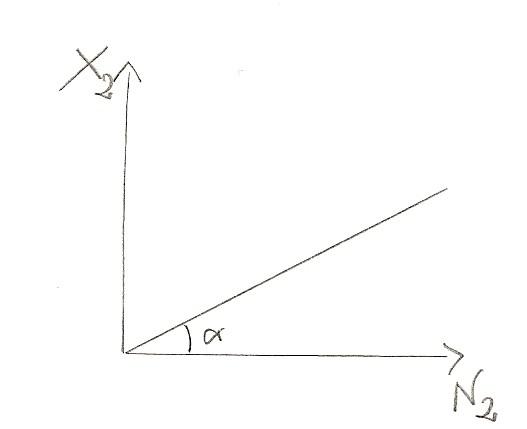
La funzione di produzione del B2 è necessariamente a rendimenti costanti. Perciò è data da:
X2 = α*N2
[In cui α sono rendimenti di scala costanti]
E il grafico sarà:
Nona equazione
Questa equazione mi trova l'occupazione totale del sistema economico, che è data da:
N = N1+N2
Decima equazione
Per garantire che non ci siano squilibri e per evitare che vi siano fughe di occupati e di capitale da un settore all'altro dobbiamo fare in modo che il salario sia lo stesso nei due settori. Perciò:
W = x*p1
Undicesima equazione
E dobbiamo fare in modo che anche il saggio di profitto sia lo stesso nei due settori. Perciò se il saggio di profitto è dato dal ROE che è uguale a profitto/capitale circolante allora:
π = (p1P1+p2P2)/p1K
[Nota: dobbiamo ricordarci che i settori operano in concorrenza perfetta e in cui i prezzi dei fattori produttivi sono uguali nei due settori]
Dodicesima equazione
Il profitto nel settore del bene di lusso sarà dato da:
p2P2 = X2p2-N2W
Il salario W è espresso in termini monetari perchè vi sia equilibrio nei settori deve essere, come già detto, lo stesso nei due settori.
Tredicesima equazione
Questa è l'equazione relativa al COSTO DI PRODUZIONE.
Poichè vi sia equilibrio nel sistema socioeconomico occorre che i costi medi di produzione nei 2 settori si eguaglino. La funzione perciò è:
(p2*X2)/N2 = (p1*X1 - p1*R) /N1
Quattordicesima equazione
Questa è l'equazione del SISTEMA DEI PREZZI.
Per fare ciò si individua il bene numerario e si fissa un prezzo che sarà pari a 1 a maggiore unità di bene in più:
α*p2 = 1
Ricordiamoci inoltre che il prezzo di un bene è il reciproco del PMa. In questo caso è: p2 = 1/α
Quindicesima equazione
E' la FUNZIONE DI DOMANDA.
Come faccio in un sistema con due mercati a descrivere una funzione di domanda? Mi basta descrivere semplicemente uno dei due settori.
Nel caso del settore dei beni di lusso (B2) Ricardo dice che tutto ciò che vi viene prodotto è acquistato solo dagli aristocratici, ossia i proprietari terrieri.
Ma quanto possono spendere questi? La rendita reale.
E quanto viene prodotto nel settore 2? X2, che espresso in valore è pari a (p2*X2). Quindi se i proprietari terrieri acquistano tutto il bene 2 prodotto in un dato periodo allora:
p2X2 = p1R
Facciamo una sintesi:
Otteniamo così un sistema di 15 equazioni a 15 incognite alla cui soluzione corrisponde l'equilibrio del sistema socio-economico
Per far funzionare il sistema dobbiamo prendere per buone alcune ipotesi costruttive:
Se tutte queste ipotesi sono vere la conseguenza è che il prezzo del grano al crescere della produzione (per l'impiego di nuovi terreni) tende a salire.
Se il prezzo del grano cresce:
π = (p1P2+p2P2)/p1K
Perchè aumentando il denominatore (perchè W aumenta K), π tende a diminuire.