Torna alla pagina di Ricerca Operativa
:: Ricerca Operativa - Esercizi di laboratorio ::
Esercizio 1: Patate
Un’azienda produce pacchi di patatine surgelate sia a bastoncino (A) che in pezzi più piccoli (B) e di fiocchi surgelati per il puré (C). L’azienda acquista da due produttori (1 e 2) con rese differenti.
| Produttore | A | B | C |
| 1 | 20% | 20% | 30% |
| 2 | 30% | 10% | 30% |
Tutto ciò che viene da 1 si trasforma per il 20% in A, 20% in B e 30% in C.
Tutto ciò che viene da 2 si trasforma per il 30% in A, 10% in B e 30% in C.
L’avanzo del 30% per entrambi i produttori è lo scarto non recuperabile.
Il profitto dell’azienda è di 2 centesimi di Euro per ogni chilogrammo di patate provenienti dal produttore 1 e di 3 centesimi/Kg per quelle provenienti dal produttore 2.
Ci sono delle limitazioni alle quantità massime di ciascun tipo di prodotto: 6 tonnellate di A, 4 di B e 8 di C.
| P = 2 | produttori | |
| N = 3 | prodotti | |
| aij | resa del prodotto j (1, ... , N) per il produttore i (1, ... , P) | [%] |
| bi | profitto corrispondente al produttore i (1, … , P) | [cent/kg] |
| lj | limiti di produzione per il prodotto j (1, ... , N) | [ton] |
| xi ≥ 0 | quantità acquistata dal produttore i (1, ... , P) | [ton] |
Notare il maggiore uguale a 0, condizione necessaria dato che non posso acquistare una quantità negativa di prodotto.
Per quanto riguarda le unità di misura in questo caso non sono così vincolanti, dipende se voglio un calcolo più veloce per verificare i limiti di produzione o per ricavare il profitto. A seconda della scelta che faccio dovrò convertire le unità di misura dei dati interessati.
| ∑i aij • xi ≤ lj | per ogni j = 1, ... , N e con i = 1, … , P | [ton] |
Massimizzare il profitto, ovviamente.
| max ∑i bi • xi • 10 | [€] |
Osservazioni da fare:
Le variabili sono variabili continue.
I vincoli sono espressi con un polinomio di primo grado, quindi il modello è lineare.
La funzione obiettivo è espressa con un polinomio di primo grado, quindi il modello è lineare.
Riassumendo: è un problema di programmazione lineare.
! Esercizio "Patate" ! Variabili: x(i) = quantità acquistata dal produttore i = 1, ... , 2 [ton] ! Le variabili sono continue e non negative ! Funzione obiettivo: massimizzazione dei profitti [Euro] max 20 x1 + 30 x2 subject to ! Vincoli sul limite massimo di produzione [ton] Limite1) 0.2 x1 + 0.3 x2 <= 6 Limite2) 0.2 x1 + 0.1 x2 <= 4 Limite3) 0.3 x1 + 0.3 x2 <= 8 End |
Cliccando sul pulsante della risoluzione (il bersaglio) appare la seguente finestra di riepilogo:
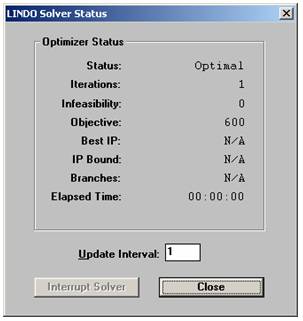
Cosa indicano i campi?
Status: in questo caso indica che ha trovato la soluzione ottima
Iterations: gli è bastato fare un unico cambio di base per trovare la soluzione
Infeasibility: non è inammissibile trovare la soluzione
Objective: risultato della funzione obiettivo
Best IP – IP Bound – Branches: sono usati solo per i problemi non lineari
Elapsed time: il tempo impiegato
LP OPTIMUM FOUND AT STEP 1
OBJECTIVE FUNCTION VALUE
1) 600.0000
VARIABLE VALUE REDUCED COST
X1 0.000000 0.000000
X2 20.000000 0.000000
ROW SLACK OR SURPLUS DUAL PRICES
LIMITE1) 0.000000 100.000000
LIMITE2) 2.000000 0.000000
LIMITE3) 2.000000 0.000000
NO. ITERATIONS= 1
|
Il report ci dice che la funzione obiettivo (z) è 600, che abbiamo 5 variabili e 3 vincoli.
Le variabili sono x1 = 0 , x2 = 20 , x3 = 0, x4 = 2 , x5 = 2.
Dato che le variabili fuori base valgono 0, ne abbiamo due fuori base {1,3} e tre in base: {2,4,5}.
Notare che se una variabile fuori base con costo ridotto 0 entrasse in base, la variazione della funzione obiettivo sarebbe pari a 0.