Swappa : Uni / Ricerca Operativa - PNL - Atomi

Torna alla pagina di Ricerca Operativa

 :: Ricerca Operativa - PNL - Atomi - 24.07.07 ::

Testo del problema

Nell’intorno di un atomo l’energia di interazione tra l’atomo stesso e un altro atomo “sonda” che gli viene avvicinato è dato dalla formula

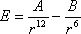
dove A e B sono parametri caratteristici dell’atomo mentre r è la distanza Euclidea tra l’atomo e la sonda. E’ data una configurazione tridimensionale di alcuni atomi, supposti puntiformi e si vuole trovare il punto di minima energia a cui la sonda (anch’essa supposta puntiforme) tende a stabilizzarsi per effetto delle interazioni con gli atomi stessi. Formulare il problema, classificarlo e risolverlo con i dati del file ATOMI.TXT.

Dati

Gli atomi sono 10.
Le posizioni degli atomi sono le seguenti:

Atomo		 x	 y	 z
 1		3.2 	2.5	4.8
 2		2.1	3.7 	8.4
 3		7.5 	2.5 	5.0
 4		6.6 	1.2 	4.5
 5		0.8 	5.1 	5.6
 6		6.3 	8.8 	3.5
 7		2.4 	1.0 	3.1
 8		1.2 	4.6 	9.0
 9		8.5 	7.8 	1.5
10		4.1 	9.3 	0.9

I valori dei parametri A e B sono i seguenti:

Atomo   1   2   3   4   5   6   7   8   9  10
  A    1.0 1.1 2.1 3.0 0.5 0.2 0.8 1.1 1.5 1.7
  B    200 400 320 250 400 200 120 300 100 500

Formulazione del problema

Dati

atomi = 10 (numero di atomi)
assi = 3 (numero di assi che compongono una coordinata)
coord_ij (coordinata dell'atomo i=1..10 sull'asse j=1..3)
parA_i (valore del parametro A per l'atomo i=1..10)
parB_i (valore del parametro B per l'atomo i=1..10)

Variabili

x_j (coordinate della sonda sugli assi indicati da j=1..3)

La variabile è libera.

Funzione obiettivo

Vogliamo minimizzare l'energia a cui la sonda tende a stabilizzarsi. Questo valore si calcola come la somma dei contributi dati all'energia da tutte le interazioni con gli atomi.

min (somma)_i [(parA_i / r12_i) – (parB_i / r6_i)]

Notare che abbiamo introdotto le due variabili ausiliarie r12 ed r6, che definiremo poi come vincoli di uguaglianza.

Vincoli

vincolo per definire r12 come la distanza euclidea tra l'atomo i e la sonda:
'''r12 = [(somma)_j (x_j – coord_ij)²]⁶ (per ogni i)
vincolo per definire r6 come la distanza euclidea tra l'atomo i e la sonda:
'''r6 = [(somma)_j (x_j – coord_ij)²]³ (per ogni i)

Linghizzazione del problema

! problema - Atomi;

model:

sets:
atomo /1..10/: parA, parB, r12, r6;
assi /1..3/: x;
posizione (atomo,assi): coord;
endsets

data: 
parA = 1.0 1.1 2.1 3.0 0.5 0.2 0.8 1.1 1.5 1.7;
parB = 200 400 320 250 400 200 120 300 100 500;
coord =	3.2 2.5 4.8
	2.1 3.7 8.4
    	7.5 2.5 5.0
    	6.6 1.2 4.5
    	0.8 5.1 5.6
    	6.3 8.8 3.5
    	2.4 1.0 3.1
    	1.2 4.6 9.0
    	8.5 7.8 1.5
    	4.1 9.3 0.9;
enddata

! funzione obiettivo;
min = @sum(atomo(i): (parA(i)/r12(i)) - (parB(i)/r6(i)));

! vincolo per definire r12;
@for(atomo(i): r12(i) = (@sum(assi(j): (x(j)-coord(i,j))^2))^6);

! vincolo per definire r6;
@for(atomo(i): r6(i) = (@sum(assi(j): (x(j)-coord(i,j))^2))^3);

! dichiarazione variabile libera x;
@for(assi(j): @free(x(j)));

end

Torna alla pagina di Ricerca Operativa