Ricerca Operativa - PNL - Scorte - 04.04.07

Torna alla pagina di Ricerca Operativa

---

 :: Ricerca Operativa - PNL - Scorte - 04.04.07 ::

Testo del problema

L’ufficio approvvigionamenti di una grande impresa deve stabilire i contratti di fornitura per uno dei suoi numerosi magazzini. Al magazzino devono pervenire periodicamente alcuni differenti tipi di materie prime e di semilavorati, provenienti ciascuno da un fornitore diverso. Per ogni tipo di merce da immagazzinare è stato calcolato quale sarebbe il periodo ottimale per minimizzare i costi di immagazzinamento.
Il problema è che tali periodi sono tutti diversi uno dall’altro e non sono multipli fra loro e quindi, se fossero rispettati, provocherebbero un continuo afflusso di fornitori al magazzino ogni giorno della settimana. L’ufficio invece vorrebbe pianificare i rifornimenti mantenendoli periodici ma in modo da farli arrivare sempre lo stesso giorno della settimana (eventualmente non tutti ogni settimana). L’obiettivo è di minimizzare i costi, sapendo che per ogni prodotto i vale la formula:

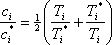
dove c(i) è il costo di magazzino relativo alla merce i, c*(i) è il costo ottimo, T(i) è il periodo di rifornimento della merce i e T*(i) è il periodo ottimo.
Formulare il problema, classificarlo e risolverlo con i dati del file SCORTE.TXT.

Dati

Le merci sono 7.
I loro periodi ottimi sono i seguenti:

Merce	    Periodo ottimo
		[giorni]
 A		  17
 B		  10
 C		  19
 D		  12
 E		   5
 F		  12.5
 G		  24

I costi ottimi corrispondenti sono i seguenti:

Merce		Costo ottimo
	    [KEuro/settimana]
 A		   140
 B		    65
 C		   200
 D		   115
 E		    75
 F		   145
 G		   100

Formulazione del problema

Dati

• merce = 7 (numero di merci)
• perOtt_i (periodo ottimo della merce i=1..7) [giorni]
• cosOtt_i (costo ottimo della merce i=1..7) [migliaia di € / settimana]

Variabili

• x_i (periodo di rifornimento della merce i=1..7)

La variabile è intera.

Funzione obiettivo

Bisogna minimizzare i costi, e possiamo ricavare la formula per calcolarli da quella data nel testo (in cui sono indicati come c_i).
Introduciamo la variabile ausiliaria per_i, che definireni poi nei vincoli:
min (somma)_i cosOtt_i * 1/2 * (per_i / perOtt_i + perOtt_i / per_i)

Vincoli

Dobbiamo fare in modo che il periodo da scegliere per ogni merce sia multiplo di una settimana, quindi di 7 giorni, ed è proprio per questo motivo che non abbiamo potuto inserire direttamente la x_i nella funzione obiettivo ma abbiamo dovuto introdurre la seguente variabile ausiliaria:
per_i = x_i * 7 (per ogni i)

Linghizzazione del problema

! problema - Scorte;

model:

sets:
merce /1..7/: perOtt, cosOtt, per, x;
endsets

data:
perOtt = 17 10 19 12 5 12.5 24;
cosOtt = 140 65 200 115 75 145 100;
enddata

! funzione obiettivo;
min = @sum(merce(i): 
	   cosOtt(i) * 1/2 * (per(i)/perOtt(i) + perOtt(i)/per(i)));

! vincolo che rende il periodo multiplo di 7 giorni;
@for(merce(i): per(i) = x(i) * 7);

! dichiarazione variabile intera x;
@for(merce(i): @gin(x(i)));

end

---

Torna alla pagina di Ricerca Operativa