Swappa :: Ricerca Operativa - Programmazione lineare intera

:: Ricerca Operativa - Programmazione lineare intera ::

Tutte le immagini di questa pagina sono prese dalle slide del prof Giovanni Righini

Introduzione

Finora abbiamo studiato problemi di programmazione lineare nel continuo, in cui cioè le variabili possono assumere valori reali. I problemi di programmazione lineare intera hanno invece variabili con valori nel dominio del discreto, ed hanno forma standard:

Il terzo vincolo è quello che mi indica che sono in un dominio dicreto non negativo.

Due casi particolari:

se alcune variabili sono continue e altre intere si parla di mixed integer programming
se le variabili sono binarie (cioè le x possono assumere solo valore 0 o 1) abbiamo invece la binary programming

Salvo poche eccezioni conosciute, la complessità computazionale di un problema di PLI è maggiore di quella della PL continua. Si tratta infatti di problemi NP-HARD, che però si rivelano molto potenti da un punto di vista modellistico.

Rilassamento continuo

La prima cosa che ci serve capire per risolvere un problema di programmazione lineare intera è il suo rilassamento continuo, ovvero il problema di programmazione lineare che si otterrebbe trascurando i vincoli di integralità. Si può pensare al rilassamento continuo come all'anello di congiunzione tra PL e PLI.

L'insieme delle soluzioni ammissibili nel discreto (X_PLI) sono un sottoinsieme di quelle che si trovano nel rilassamento continuo (X_PL), di conseguenza la funzione obiettivo non cambia e la regione ammissibile è soltanto allargata. Per quanto riguarda la soluzione ottima distinguiamo due casi:

se stiamo massimizzando: z_PL >= z_PLI
se stiamo minimizzando: z_PL <= z_PLI

Se scopriamo che la z_PL è intera, allora quella soluzione è ottima anche per il problema intero. Ma se intera non lo è, non potremmo semplicemente risolvere il problema PLI arrotondandola all'intero più vicino? No, perché ci sarebbero troppi casi in cui questa strada porterebbe a risultati molto lontani dall'ottimo, se non addirittura fuori dalla regione ammissibile. Guarda l'esempio sotto per credere:

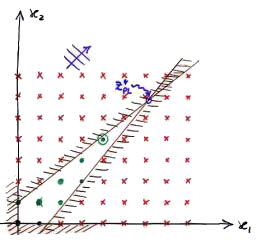
La differenza che passa tra il risolvere un problema nel continuo ed uno nel discreto è misurabile, e l'unità di misura utilizzata per quantificarla è l' integrality gap dato da z_PL - z_PLI. Si tratta di un indice che dà informazioni sulla difficoltà del problema e sulla sua bontà di formulazione. Questa ha infatti caratteristiche diverse rispetto al continuo, una su tutte il fatto che lo stesso problema intero può essere definito con molte formulazioni diverse (diversi vicoli, anche in numero). In generale la formulazione migliore è quella che ha i vincoli corrispondenti agli iperpiani (chiamati faccette) che definiscono il guscio convesso (convex hull) delle soluzioni ammissibili intere. Fermi tutti, di cosa stiamo parlando? Stiamo dicendo che dobbiamo fissare i vertici del poliedro su coordinate intere, così che la regione ammissibile possa essere il più stringente possibile. Ciò è molto utile perché se riusciamo a descrivere un problema di programmazione lineare intera come guscio convesso dei suoi punti interi, allora siamo anche in grado di utilizzare l'algoritmo del simplesso per calcolare l'ottimo: risolvendo la PL risolveremmo anche la PLI!
Tutto questo è molto bello, ma accade molto raramente.

Il rilassamento continuo non è l'unico tipo di rilassamento possibile. Abbiamo anche:

rilassamento surrogato, che si ottiene facendo una combinazione lineare di due o più vincoli del sistema, ad esempio sommandoli. Il motivo per cui si riesce a diminuire il numero di vincoli è che tutte le soluzioni che soddisfano quelli di partenza soddisfano anche la loro combinazione lineare, mentre non è vero il viceversa. Notare che anche questo tipo di rilassamento allarga la regione ammissibile
rilassamento combinatorio, che si ottiene quando elimino i vincoli di subtour elimination constructor (???)
rilassamento LaGrangiano, che non consiste nell'ignorare un vincolo, ma nel toglierlo direttamente dal sistema e penalizzarne la violazione modificando la funzione obiettivo

Indipendentemente dal tipo di rilassamento che decideremo di usare, l'obiettivo è ottenere il più piccolo integrality gap possibile, così da migliorare la facilità del problema.

Branch-and-bound

Branching

Una tecnica che fa uso di tutte queste informazioni e strategie e che funziona sempre si chiama Branch-and-bound e consente di trovare la soluzione ottima di problemi combinatori NP-HARD. Nota bene prima di cominciare: si tratta di un sistema per progettare algoritmi, ma non è un algoritmo.

L'idea più semplice per trovare le soluzioni di problemi combinatori nel discreto è enumerarle tutte, tanto saranno sicuramente un numero finito. Ok, l'idea è semplice, ma impraticabile: elencare esplicitamente una soluzione alla volta impiegherebbe un tempo di calcolo potenzialmente esponenziale, quindi impensabile nella maggior parte dei casi.

L'alternativa è enumerarle implicitamente, così da considerarle tutte ma senza elencarle una per una. Come si fa? Dato un problema P con regione ammissibile X(P) si partiziona quest'ultima in tanti sottoinsiemi, ovvero si generano più problemi figli (più facili) a partire da un problema padre. Se sono in grado di risolverli allora potrò confrontarne le soluzioni per scegliere quella migliore, altrimenti li scompongo ricorsivamente in nuovi figli.
Quest'operazione di partizionamento o biforcamento prende il nome di branching, e genera un albero chiamato albero di decisione (decision tree) il cui numero di nodi cresce in modo esponenziale man mano che scendiamo di livello. La foglia dell'albero è quindi la base della ricorsione, e corrisponde o a un sottoproblema talmente elementare che possiamo ricavare subito la soluzione, o a un sottoproblema inammissibile.
Nota di folklore: più che un albero è un'alborescenza dato che è limitato ed ha solo archi orientati.

L'operazione di branching deve essere fatta con attenzione, rispettando alcune precise condizioni. Per prima cosa deve garantire la correttezza, che mi permette di essere sicuro di aver enumerato implicitamente tutte le soluzioni del problema. Questa proprietà si esprime formalmente dicendo che l'unione delle regioni ammissibili di tutti i figli deve corrispondere a quella del padre. In formula:

In secondo luogo voglio raggiungere l'efficienza facendo in modo che le regioni ammissibili dei figli siano disgiunte, o altrimenti una stessa soluzione potrebbe essere contenuta in più di un problema figlio, e quindi verrebbe considerata più volte. Questa seconda condizione si esprime dicendo che l'intersezione delle regioni ammissibili di due figli diversi sia nulla. In formula:

Come si fa a fare branching? Tipicamente possiamo seguire due strategie: aggiungere vincoli o fissare variabili. Vediamo gli esempi che il prof Righini ha fatto sulle sue slide:

1	2
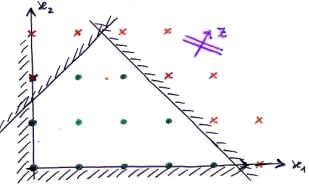
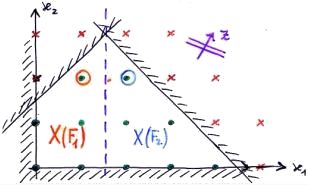
Problema lineare con due vincoli nel discreto.	Faccio branching aggiungendo un vincolo, dividendo così il padre in due figli.
3	4
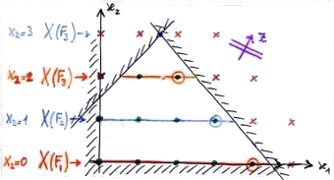
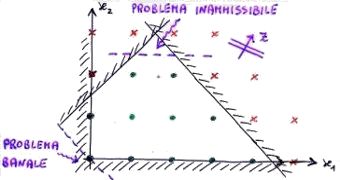
Faccio branching fissando variabili, generando quattro figli che hanno come regione ammissibile tutti i punti su una retta.	Esempi di problemi inammissibili o banali, che rappresentano la base della ricorsione.

Abbiamo detto un po' di parolone e introdotto qualche concetto, ma non montiamoci la testa: limitarsi a creare quest'albero senza fare nessun altro tipo di intervento equivale ad effettuare un'enumerazione esplicita! Infatti tutto ciò che abbiamo detto finora è che dobbiamo arrivare alle foglie per raggiungere la base della ricorsione, ma dato che queste sono pari al numero di soluzioni del problema originario non abbiamo fatto alcun passo avanti. Ecco perché il metodo del branch-and-bound non si chiama solo branch, ma c'è anche il...

Bounding

Il bounding è quell'attività che associa ad ogni sottoproblema una stima del valore ottimo, fatta per eccesso se stiamo massimizzando o per difetto in caso contrario, chiamata bound duale. Perché mi serve? Perché tutte le volte che grazie al bound duale scopro che il valore ottimo che potrei raggiungere espandendo tutto il sottoalbero di un certo nodo P non è migliore di una certa soluzione che conosco già, allora posso fare benissimo a meno di espanderlo risparmiando tempo e memoria.
Abbiamo quindi bisogno di una soluzione nota che faccia da termine di paragone, e dato che si tratta di un'approssimazione può essere ad esempio calcolata con un algoritmo euristico; va da sé che più è vicina all'ottimo e più sarà utile. Una volta trovata, associo un bound ad ogni nodo (che ricordiamo corrisponde a un sottoproblema P) e lo confronto con la soluzione nota. Abbiamo due possibili casi:

se sto minimizzando, il bound duale è un lower bound (LB), cioè un limite inferiore. Indica quanto posso sperare di scendere con la soluzione enumerando tutte le soluzioni di P
se sto massimizzando, il bound duale è un upper bound (UB)

In formula:

dove con "P chiuso" si intende che posso fare a meno di esplorare il nodo P.

Ricapitolando, per fare bounding dobbiamo necessariamente conoscere una soluzione ammissibile di paragone ed un algoritmo per calcolare il bound duale di ogni sottoproblema.
Le prestazioni computazionali complessive del branch-and-bound dipendono molto dall'efficacia di questa sua seconda fase.

Commentiamo la figura a destra.
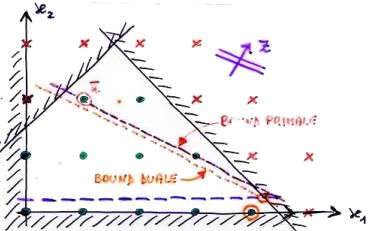Abbiamo diviso il problema in due sottoproblemi aggiungendo un vincolo, quello orizzontale in basso tracciato in viola. Consideriamo la parte inferiore. Per risolverlo come problema di programmazione lineare calcoliamone il rilassamento continuo: dopo opportuni calcoli abbiamo scoperto che l'ottimo va a finire sul cerchietto in rosso, ed ha come curva di livello della funzione obiettivo in quel punto quella obliqua di colore arancione. Questa rappresenterà il bound duale, perché è una stima per eccesso di quanto può valere nel migliore dei casi l'ottimo di quel sottoproblema: nessun'altra soluzione ammissibile del figlio potrà valere di più.
Supponiamo ora che un'euristica abbia calcolato come soluzione di paragone quella segnata con x' (x trattino): il suo valore è il bound primale e corrisponde alla curva di livello obliqua tracciata in viola. Come possiamo facilmente vedere, la curva del bound duale si trova sempre sotto quella del bound primale, quindi tutte le soluzioni del sottoproblema inferiore sono peggiori di x'. Posso perciò ignorare tranquillamente quel sottoproblema, tanto non migliorerà mai la soluzione nota.

Ecco dunque perché è utile avere una buona euristica, per essere indicativa nello scartare i sottoproblemi non utili.

Esplorazione dell'albero

Un'altra componente importante dell'algoritmo branch-and-bound è la strategia di esplorazione dell'albero, poiché non è possibile esaminare simultaneamente tutti i problemi figli di ogni problema padre in parallelo. La searching strategy stabilisce un ordinamento dei sottoproblemi aperti e quindi una politica di esplorazione, ed incide molto sulle prestazioni dell'algoritmo, in particolare sulla quantità di memoria utilizzata più che sul tempo.

Componenti fondamentali del branch-and-bound

Tirando le somme, i quattro componenti fondamentali per gli algoritmi di tipo branch-and-bound sono:

la regola di branching, che usiamo per partizionare ogni problema in sottoproblemi
l'algoritmo di calcolo del bound duale
l'algoritmo di calcolo del bound primale
la strategia di esplorazione dell'albero

Vediamo alcuni esempi per ognuno di essi.

Regole di branching

su variabile binaria, che genera alberi binari. E' quella usata anche da Lindo
su vincolo intero, che genera un albero binario un po' diverso da quello precedente, dato che nel primo caso fissiamo una variabile mentre qui stiamo introducendo un vincolo
su variabile intera, che genera alberi n-ari fissando una variabile
su M variabili binarie

Calcolo del bound duale

In genere il bound duale si calcola o risolvendo all'ottimo un rilassamento, o trovando una soluzione ammissibile ad un problema duale. Nel secondo caso, se stiamo massimizzando, l'idea è trovare una soluzione che sia maggiore uguale dei valori ammissibili del problema primale; in altre parole significa calcolare l'UB.

Rivediamo le principali tecniche di rilassamento:

rilassamento lineare/continuo
rilassamento surrogato, ottenuto combinando linearmente diversi vincoli lineari in un unico vincolo lineare
rilassamento lagrangeano, che elimina alcuni vincoli penalizzandone la violazione aggiungendo termini alla funzione obiettivo

Calcolo del bound primale

Il bound primale si può calcolare nei seguenti modi:

con un algoritmo di approssimazione (quindi euristico) da far partire prima del branch-and-bound
arrivando a una qualsiasi foglia durante l'esplorazione dell'albero
eseguendo un algoritmo euristico di approssimazione in ogni nodo. Questa via sarà la più sicura e affidabile ma è poco ottimizzata

Strategia di esplorazione

Concludiamo citando le principali strategie di esplorazione dell'albero decisionale:

"depth-first-search" (in profondità): ogni volta che un padre genera i figli li ordina in qualche modo, poi prende il primo e lo espande; il tutto avviene ricorsivamente mentre gli altri aspettano. Non richiede troppa memoria dato che deve memorizzare solo i nodi in sospeso, e arrivando velocemente alla foglia trova il bound primale relativamente presto. E' una strategia molto utile se non abbiamo euristiche a disposizione
"best-first-search": si ordinano i nodi in modo da esplorare per primi quelli più promettenti, guardando i loro bound duali
metodi ibridi, che passano da una tecnica all'altra in run-time

Relazioni tra componenti

Ognuno di questi componenti è indipendente dal punto di vista della correttezza, ma sono in stretta relazione per quanto riguarda l'efficienza (o meglio ancora, l'efficacia)! Nel realizzare un algoritmo branch-and-bound dovremmo infatti tenere conto di alcune cose (ricopiate dalle slide di Righini):

"se il calcolo del bound duale produce una soluzione ammissibile del sottoproblema in esame, essa ne è anche la soluzione ottima. Quindi il sottoproblema è già risolto e non richiede branching. La soluzione ottima del sottoproblema è un bound primale"
"il calcolo del bound duale può fornire quasi gratis anche un bound primale (euristiche lagrangeane)"
"la politica depth-first fornisce più in fretta dei buoni bounds primali"
"la 'miglior' strategia di branching è quella che produce la maggior variazione nei bounds duali associati ai nodi figli"

Inoltre osserviamo che nel passaggio dal padre al figlio il bound duale si stringe sempre di più dal momento che quest'ultimo diventa sempre più vincolato (da un nuovo vincolo o da una variabile fissata). Il bound primale è invece calcolato con euristiche, e dato che può essere aggiornato se ne trovo di migliori, il suo valore non può peggiorare durante l'esplorazione dell'albero.

Branch-and-bound troncato

Abbiamo già detto che il tempo di calcolo del branch-and-bound non è garantito polinomiale (è NP-HARD), quindi utilizzarlo così com'è per risolvere problemi di grandi dimensioni ci farà correre il rischio di non vivere abbastanza per vedere il risultato. L'idea è quella di troncarlo (interromperlo) dopo un certo periodo di tempo dall'inizio o dall'ultimo miglioramento trovato, tanto se abbiamo adottato una buona strategia di esplorazione ed abbiamo calcolato i bound in modo intelligente, avremo buone probabilità che l'algoritmo riesca a trovare rapidamente la soluzione ottima. Ovviamente questo ha un prezzo, ovvero la perdita della garanzia di ottimalità, la sua certezza assoluta.

Se però non cerchiamo l'ottimalità a tutti i costi, il troncamento non è l'unico metodo per velocizzare il branch-and-bound: un secondo sistema consiste nel modificare il test di chiusura di un nodo. Quello classico è (se stiamo minimizzando):
LB(P) >= z(x') ; mentre quello più veloce è LB(P) >= α * z(x'), con 0<α<1 che rende più probabile l'eventualità che il test abbia successo. Otteniamo in questo modo un algoritmo 1/α approssimante, in cui più è piccolo α e più facile diventerà la chiusura di un nodo.

Applicazione

Come si applica un branch-and-bound in un problema di programmazione lineare intera? Semplice! Andatevi a vedere le slide del professore dalla Lezione8_22 alla Lezione8_24.

Altre tecniche

Esistono altre tecniche che consentono di risolvere problemi di PLI senza ricorrere al branching, ma lavorando direttamente nel nodo radice e continuando a risolvere iterativamente sottoproblemi lineari interi sempre più vincolati. Questi metodi sono chiamati piani di taglio (cutting planes), ed un esempio è quello di Gomory.

Possiamo combinare questi metodi con il branch-and-bounds dando origine al simpaticissimo branch-and-cut, che sfortunatamente non vedremo.

Torna alla pagina di Ricerca Operativa