cerca
Appello d'esame di Elaborazione delle Immagini - 17/07/2006
modifica cronologia stampa login logout

Wiki

UniCrema


Materie per semestre

Materie per anno

Materie per laurea


Help

Appello d'esame di Elaborazione delle Immagini - 17/07/2006

Torna alla pagina di Elaborazione delle Immagini 

 :: Appello d'esame di Elaborazione delle Immagini - 17/07/2006 ::

Esercizio 1

Guardando l’immagine mostrata in Figure 1:

  1. Indicare approssimativamente i passaggi morfologici che portano da (a) a (b).
  2. Indicare approssimativamente i passaggi morfologici che portano da (b) a (c).
  3. Cosa si è ottenuto alla fine del processo.
  4. Indicare una possibile alternativa al processo indicato.

SOLUZIONE

1- E' stata effettuata la differenza fra (a) e la versione di (a) su cui è stato effettuato un thinning con un'ellisse il cui asse minore è maggiore di 200 pixel

2- altro processo di thinning con ellisse di asse maggiore che deve essere maggiore di 250 pixel

3- Con questo processo abbiamo separato il volto della Gioconda dallo sfondo.

4- Un altro procedimento che avrebbe permesso di separare il volto dallo sfondo è la trasformazione hit-or-miss, che è una trasformazione morfologica fondamentale per l'individuazione della forma.
Ricordiamo che questa trasformazione si basa sulle seguenti operazioni:
- erosione dell'insieme A attraverso D, dove A contiene D e D è l'oggetto di nostro interesse
- erosione del complemento di A attraverso (W-D), dove W è una piccola finestra che racchiude D e la loro differenza viene definita sfondo locale
- l'intersezione tra queste due erosioni permette di ottenere D, nel nostro caso il viso della Gioconda.

Esercizio 2

Data l’immagine rappresentata in Figure 2, calcolarne:

  1. l’istogramma;
  2. la probabilità dei livelli di grigio
  3. la codifica LZW

SOLUZIONE

1- 8 livelli di 1, 4 livelli di 5, 4 livelli di 2.
L'istogramma ovviamente approssimativo dell'immagine è:

Ricordiamo che l'istogramma di un'immagine digitale con livelli di intensità nella gamma [0, L-1] è una funzione discreta h(rk)=nk dove rk è il valore d'intensità k-esimo ed nk è il numero di pixel dell'immagine con intensità rk.

2- La probabilità dei livelli di intensità è: p(rk)=nk/MN dove M e N sono le dimensioni dell'immagine.
Nel nostro caso avremo che:
l'immagine la consideriamo come una 4X4 e quindi
p(1) = 8/16 = 1/2 = 0.5
p(2) = 4/16 = 1/4 = 0.25
p(5) = 4/16 = 1/4 = 0.25

3-

NUOVO CARATTERE

STRINGA CORRENTE

OUTPUT

DIZIONARIO

1

1

1

11

1

11 -> 8

1

11

1

111

8

111 -> 9

5

15

1

15 -> 10

5

55

5

55 -> 11

5

55

5

555

11

555 -> 12

2

52

5

52 -> 13

2

22

2

22 -> 14

2

22

2

222

14

222 -> 15

1

21

2

21 -> 16 (ma non lo consideriamo)

1

11

1

111

1

1111

9

1111 -> 17 (ma non lo consideriamo)

1

1

Quindi avremo come output: 1, 8, 1, 5, 11, 5, 2, 14, 2, 9, 1
Buttiamo fuori 11 simboli da 4 bit: 11 * 4 = 44 bit, all'inizio invece erano 16 * 3 = 48 bit; abbiamo guadagnato poco con la compressione.

In questo caso abbiamo scelto di utilizzare un dizionario da 4 bit, in quanto i valori iniziali dell'immagine li abbiamo considerati da 0 a 7 (i valori di intensità infatti sono soltanto 1, 2, 5), quindi 3 bit. Per questo motivo gli ultimi due valori del dizionario non li abbiamo considerati, dovremmo utilizzare un dizionario più grosso per poterli utilizzare.

Un'ottima guida che spiega passo passo come risolvere la compressione LZW si trova al seguente link: LZW

Esercizio 3

Data l’immagine mostrata in Figure 3, descrivere di che problema è affetta. Proporre un rimedio, darne una descrizione almeno a livello teorico.

SOLUZIONE

L'immagine è affetta da motion blur, quindi da effetto "mosso".
I due fattori principali che provocano questo effetto sono:

  • tempo di esposizione
  • velocità a cui si spostano gli oggetti o le persone inquadrate

Infatti la quantità di sfocatura è direttamente proporzionale alla velocità del soggetto ed ai tempi di esposizione.
Dal punto di vista tecnico per limitare questo effetto bisogna ridurre il tempo di esposizione ed utilizzare un cavalletto.
Dal punto di vista del corso, un piccolo miglioramento è possibile ottenerlo tramite i filtri spaziali di sharpening che rendono più nitida l'immagine evidenziando le zone sfocate; l'immagine però è troppo sfocata e difficilmente si riesce con questo metodo ad ottenere qualcosa di decente.

Esercizio 5

Data l’immagine della Figure 4:

  1. Filtrarla con il filtro rappresentato nella Figure 5.
  2. Di che filtro si tratta?
  3. Cosa si ottiene filtrando l’immagine?

1- filtrando l'immagine otteniamo: 

     5     3     3     5
     3     0     0     3
     3   -99   -99   -96
     3   -99   792   -96
     5   -96   -96   -94

Dove vediamo che le zone costanti vengono modificate poco, mentre risalta tutta la zona attorno al 100.

2- si tratta del filtro laplaciano, che permette di effettuare lo sharpening spaziale dell'immagine, utilizzando le caratteristiche della derivata seconda.

3- il laplaciano mette in evidenza le discontinuità di intensità, mentre lascia in secondo piano le zone con livelli di intensità costante o poco variabile.
Quando si ottiene un immagine laplaciana troppo scura con molto nero è dovuto al fatto che nell’equazione ci sono sia valori positivi sia negativi e tutti i valori negativi sono ridotti a 0 dal display. Per rientrare nella gamma [0, L-1] si somma all’immagine laplaciana il suo valore minimo in modo da riportare il minimo a zero. Lo sfondo quindi da nero dovrebbe diventare grigio, per via della riscalatura delle intensità.

SOLUZIONE

Esercizio 6

Dare una descrizione operativa della trasformata di Hough per le linee rette (indicare cioè un metodo per il calcolo) ed indicarne possibili applicazioni all’elaborazione di immagine.

SOLUZIONE

La trasformata di Hough viene utilizzata nel processo di edge linking perché permette di individuare i punti che si trovano su linee rette.
Sappiamo che da un punto (xi, yi) nel piano xy passano infinite rette che soddisfano l'equazione yi=axi+b al variare di a e b. Se ora cambiamo piano e passiamo a quello ab chiamato spazio dei parametri otteniamo la seguente equazione: b=-axi+yi che rappresenta una singola retta passante per il punto (xi, yi).
Se adesso consideriamo un secondo punto (xj, yj) che nello spazio dei parametri interseca la retta associata al punto (xi, yi) nel punto (a', b'), abbiamo che questi due punti nel piano xy giacciono sulla stessa retta.

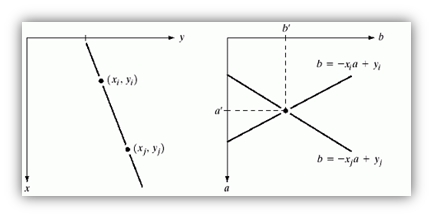
Quindi per tutti i punti che passano per la stessa retta nel piano xy passano infinite rette nello spazio dei parametri che si intersecano nel punto (a', b').
Le rette nel piano xy possono essere identificate individuando i punti nello spazio dei parametri in cui si interseca il maggiore numero di rette.
Il problema è che quando la retta si avvicina alla direzione verticale, a tende all'infinito, quindi conviene cambiare rappresentazione utilizzando la seguente equazione: xcosθ+ysinθ = ρ

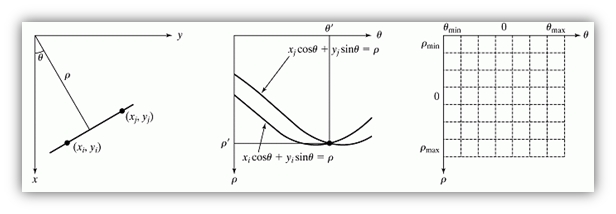
Ora ogni curva sinusoidale rappresenta l'insieme delle linee che passano per un particolare punto (x,y) nel piano xy. Il punto di intersezione (ρ',θ') corrisponde alla retta che passa per i due punti indicati precedentemente.
La terza immagine mostra le celle di accumulazione che vengono incrementate per sapere quali punti fanno parte della stessa retta.

La trasformata è possibile utilizzarla come metodo globale per l'edge linking e risulta utile quando non si ha nessuna conoscenza a priori sugli oggetti di interesse (cioè regioni e bordi), ma si ha soltanto un'immagine di edge e quindi tutti i pixel sono possibili candidati per il linking. Ad esempio se abbiamo un'immagine dove sono presenti molte strade dritte questo metodo permette di estrarle senza problemi.

Torna alla pagina di Elaborazione delle Immagini