Swappa :: Appello d'esame di Elaborazione delle Immagini

Torna alla pagina di Elaborazione delle Immagini

 :: Appello d'esame di Elaborazione delle Immagini - 11/09/2006 ::

Esercizio 1

Guardando l’immagine mostrata in Figure 1:

Indicare approssimativamente quali passaggi morfologici portano da (a) a (b).
Cosa si è ottenuto alla fine del processo.
Disegnare qualitativamente l’istogramma.

SOLUZIONE

In figura a e' mostrata un'impronta digitale in cui e' possibile notare del rumore che va a disturbare il pattern dell'impronta e crea sicuramente dei problemi al sistema biometrico.
L'immagine e' binaria ed il rumore e' presente sotto forma di elementi chiari sullo sfondo scuro ed elementi scuri sui tratti chiari dell'impronta.
La figura b mostra la stessa impronta digitale dopo essere stata sottoposta alle operazioni morfologiche: erosione, apertura, dilatazione, chiusura.
Lo scopo e' quello di preparare l'impronta per sistemi di riconoscimento automatico.

Vediamo in dettaglio i quattro passaggi:
Il primo passo di erosione ha eliminato il rumore sullo sfondo perche' le componenti del rumore sono piu' piccole dell'elemento strutturante scelto. Mentre le componenti di rumore scuro, all'interno dell'impronta, sono state ingrandite perche' questi sono dei bordi interni che crescono per l'erosione.
Il secondo passo di apertura permette di ridurre o cancellare il rumore presente, aumentato a causa dell'erosione, nell'impronta digitale. Il risultato non e' ancora soddisfacente perche' sono presenti dei vuoti tra le linee dell'impronta.
Il terzo passaggio di dilatazione permette di riunire alcune linee, correggere alcune rotture, pero' introduce il problema che le linee vengono ingrossate eccessivamente.
Il quarto passaggio di chiusura permette di eliminare il problema dell'ingrossatura delle linee.
Il risultato finale e' sicuramente migliore della situazione di partenza perche' non e' piu' presente rumore, pero' sono rimaste delle interruzioni nell'impronta che non e' stato possibile riparare.

Nell'istogramma avremo una, seppur poco consistente, minor presenza di bianco in quanto sullo sfondo non e' piu presente rumore ed e' completamente nero.

Esercizio 2

Data l’immagine rappresentata in Figure 2, calcolarne:

l’istogramma;
la probabilità dei livelli di grigio
l’entropia dell’immagine

SOLUZIONE

1- Ci sono:
- 12 livelli di intensità 1
- 3 livelli di intensità 10
- 1 livello di intensità 5

Ricordiamo che l'istogramma di un'immagine digitale con livelli di intensità nella gamma [0, L-1] è una funzione discreta h(r_k)=n_k dove r_k è il valore d'intensità k-esimo ed n_k è il numero di pixel dell'immagine con intensità r_k.

2- La probabilità dei livelli di intensità è: p(r_k)=n_k/MN dove M e N sono le dimensioni dell'immagine.
Nel nostro caso avremo che:
l'immagine è una 4X4 e quindi le probabilità sono:
p(1): 12/16 = 3/4 = 0.75
p(10): 3/16 = 0.1875
p(5): 1/16 = 0.0625

3- L'entropia è l'informazione media della sorgente di intensità immaginaria in bit, detto in parole umane la quantità media di informazione presa dalla sorgente.
Il rapporto tra l'entropia e la quantità di informazione visiva è tutt'altro che intuitivo. Cioè ci possono essere delle immagini che sembrano avere pochissima informazione visiva, ma allo stesso tempo avere un'alta entropia.
L'entropia di primo ordine si calcola tramite la seguente formula:

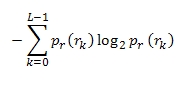
dove p_r è la probabilità dell'occorrenza del livello di intensità r_k in una immagine.

Quindi nel nostro caso avremo:
- [0.75 * log₂ 0.75 + 0.1875 * log₂ 0.1875 + 0.0625 * log₂ 0.0625] =
- [0.75 * (-0.4150) + 0.1875 * (-2.4150) + 0.0625 * (-4)] =
1.0141 bit/pixel

Esercizio 3

Data l’immagine mostrata in Figure 3(b), descrivere un metodo per rivelare la direzione dei ridge. In Figure 3(a) è mostrata la nomenclatura generalmente utilizzata nel riconoscimento delle impronte digitali.

SOLUZIONE

Una soluzione possibile è quella di utilizzare il gradiente, in quanto permette di individuare l'intensità e appunto la direzione di un edge in un certo punto. Questo è possibile perché il gradiente è un vettore bidimensionale che ha l'importante proprietà geometrica di puntare nella direzione di massima variazione di f nel punto (x,y).
La direzione del gradiente è data da:

La direzione di un edge in un punto qualsiasi (x,y) è ortogonale alla direzione α (x,y) del vettore gradiente in quel punto.
Per ottenere le componenti del gradiente è necessario utilizzare gli operatori di Roberts, di Prewitt o di Sobel.
Una volta ottenuta l'immagine gradiente, se il risultato non fosse soddisfacente è possibile utilizzare ancora il gradiente per effettuare edge-linking, quindi trovare effettivamente tutti i punti di edge ed eliminare quelli che non lo sono.
Nell'esercizio comunque non richiede un'individuazione di edge completa, ma soltanto la direzione dei ridge.

Esercizio 5

Data l’immagine della Figure 4:

Filtrarla con il filtro rappresentato nella Figure 5.
Di che filtro si tratta?
Cosa si ottiene filtrando l’immagine?

SOLUZIONE

1- filtrando l'immagine otteniamo:

     0     0     0     0
     0     1    -1     0
     0    -1     1     0
     0     1    -1     0
     0     0     0     0

2- è un filtro box di media spaziale in cui tutti i coefficienti sono uguali.

3- il filtro di media è un filtro lineare di smoothing che permette di:

sfocare l'immagine, facendo risaltare gli oggetti di interesse;
eliminare le transizioni di intensità brusche, che spesso sono associate al rumore;
eliminare i falsi contorni;
ridurre i dettagli irrilevanti;

In generale questi filtri sostituiscono il valore di ogni pixel con la media dei livelli di intensità nella regione definita dalla maschera del filtro.

Esercizio 6

Dare una descrizione delle ridondanze utilizzate per la compressione di immagine. Dare una definizione del rapporto di compressione.

SOLUZIONE

La compressione delle immagini è il processo che riduce la quantità di dati necessari per rappresentare una immagine, cioè una certa quantità di informazione. La distinzione tra dati e informazione è che i dati rappresentano l'informazione; visto che differenti quantità di dati possono rappresentare la stessa quantità di informazione, allora le rappresentazioni che contengono informazioni irrilevanti o ripetute contengono dati ridondanti.
Se supponiamo che b e b' denotano il numero di bit in due rappresentazioni della stessa informazione, la ridonanza relativa dei dati R della rappresentazione con b bit è:
R = 1 - 1/C_r

dove C è il rapporto di compressione, o coefficiente di ridondanza, ed è definito come:
C = b / b'

dove b è il file originale, mentre b' è il file compresso.

Solitamente le immagini risentono di tre tipi di ridondanza:

Ridondanza della codifica (Coding Redundancy): i codici a 8 bit che vengono utilizzati per rappresentare le intensità delle immagini contengono più bit del necessario.
Un codice è un sistema di simboli (lettere, numeri, bit) utilizzati per rappresentare una certa quantità di informazione. Ad ogni pezzo di informazione è assegnata una sequenza di simboli codificati, chiamati codeword. Il numero di simboli che costituisce ciascun codice è la sua lunghezza.
Abbiamo la presenza di ridondanza della codifica ad esempio quando viene utilizzato lo stesso numero di bit per rappresentare ogni pixel dell'immagine, anche quando le probabilità dei livelli di intensità sono diverse. La riduzione di questa ridondanza infatti cerca di assegnare ai valori di intensità più probabili codici di lunghezza inferiore, mentre ai valori di intensità meno probabili codici di lunghezza superiore.
Ricordiamo che il numero di bit utilizzato per rappresentare un'immagine è dato dal prodotto delle dimensioni dell'immagine per il numero medio di bit utilizzato per rappresentare ciascun pixel.
Ridondanza spaziale e temporale (Interpixel Redundancy): nella maggior parte delle immagini i pixel sono relazionati spazialmente (ciascun pixel è simile ai pixel del suo intorno o dipende da esso), quindi l'informazione è replicata inutilmente nei pixel correlati.
La correlazione tra i pixel deriva dalle relazioni geometriche e strutturali degli oggetti presenti nell'immagine.
La ridondanza temporale invece è presente nei video.
Questo tipo di ridondanza può essere ridotta dal mapping, una codifica che permette una rappresentazione più efficiente, ma non visiva. Questo tipo di codifica può essere reversibile se dai pixel codificati è possibile tornare all'immagine originale, irreversibile altrimenti.
Ad esempio la codifica a coppie run-length, dove un valore denota un valore di intensità mentre l'altro indica i pixel consecutivi che possiedono quel dato valore di intensità.
Informazione irrilevante (Psychovisual Redundancy): è quel tipo di informazione che nelle immagini è meno importante perché viene ignorata dal sistema visivo umano e può essere eliminata in quanto non viene ridotta la percezione qualitativa dell'immagine, perché il sistema visivo effettua una media dei valori di intensità e percepisce soltanto il valore medio e ignora le piccole variazioni di intensità. Nei vari modelli di codifica il procedimento irreversibile che permette di eliminare questo tipo di informazione è la quantizzazione; essendo irreversibile la quantizzazione (il quantizzatore) non sarà presente in quelle codifiche che devono essere lossless, cioè senza perdita di informazione.

Per quantificare la natura e la quantità di informazione persa ci sono due criteri:
- oggettivo: misura l'errore tra l'immagine di input e quella di output. E' semplice e conveniente, ma si preferisce l'altro criterio per via del fatto che alla fine le immagini vengono viste dalle persone.
- soggettivo: è il criterio piu' appropriato

La compressione si realizza quando la ridondanza viene ridotta o eliminata.

Torna alla pagina di Elaborazione delle Immagini