Torna all'introduzione - Vai alla parte 1
:: Appunti di fotografia digitale - Parte 2 ::
Linearità dei sensori
I sensori sono dispositivi lineari, ovvero a fronte di un raddoppiamento della quantità di luce raddoppiano anche le loro uscite. Se però ci sono dei pixel che saturano o che non riescono a raccogliere abbastanza fotoni avremo però delle situazioni di non-linearità nelle zone rispettivamente più chiare e più scure.
L'occhio umano non è lineare, ma tende ad amplificare le ombre e a comprimere le zone più brillanti. Ciò significa che se raddoppiassimo la quantità di luce in una scena poco illuminata percepiremmo un cambiamento molto maggiore di quello che avvertiremmo in condizioni di elevata luminosità.
Ecco due curve indicative: la prima rappresenta la linearità dei sensori, la seconda la non linearità dell'occhio (ciò che per il sensore ha valore 127 da noi viene percepito come 186).
La fotocamera riesce a compensare la visione umana applicando alla propria curva lineare una curva tonale, che assegnerà più informazioni alle zone in ombra e meno a quelle brillanti.
Nei grafici seguenti sono riportate in rosso la curva lineare, in blu la curva tonale applicata ad essa, e infine in verde la curva percepita. A sinistra il tutto è riportato su scala lineare, a destra su scala logaritmica.
Quando si scatta una foto direttamente in formato JPEG la curva tonale applicata automaticamente dalla fotocamera potrebbe tagliare alcuni dettagli delle zone più chiare e più scure, cosa che non succederebbe se si scattasse in formato raw. Queste ultime utilizzano infatti la curva tonale corretta, così che la resa visiva su monitor o su carta dell'intera gamma dinamica sia piacevole alla vista.
Istogrammi
Uno strumento importantissimo per farci comprendere la nostra immagine digitale è l'istogramma, che rappresenta sotto forma di grafico com'è distribuita la luminosità dei pixel. Ad ognuno di essi viene infatti assegnato un valore che va da 0 (nero) a 255 (bianco), così da ottenere i 256 livelli che saranno disposti sull'asse delle x e su cui verranno costruiti gli istogrammi stessi; l'altezza di questi ultimi dipende dal numero di pixel che hanno quella particolare luminosità: maggiore è il numero e più alti sono.
Vediamo un esempio:
Due osservazioni di carattere generale sul grafico:
- gli istogrammi hanno tutti un pixel di larghezza e sono attaccati tra loro poiché eventuali spazi vuoti potrebbero essere interpretati come assenza del tono corrispondente
- da sinistra a destra del grafico avremo i toni più scuri, poi i grigi intermedi, infine i toni più brillanti
Ma ai fini pratici è utile esaminare l'istogramma di un'immagine? Certo, dà importanti informazioni sull'esposizione e sulla qualità dei dettagli. Facciamo una serie di esempi:
Dagli esempi visti non vorremmo far passare l'idea che una buona immagine digitale la si riconosce da picchi bassi agli estremi e valori più alti nei mezzi toni. Questo risultato è apprezzabile (e da ricercare) nelle scene illuminate in modo piuttosto omogeneo, ma poi molto dipende dal soggetto: se la maggior parte dei suoi toni sono scuri (scene "low key") è logico aspettarsi istogrammi sbilanciati verso sinistra, altrimenti (scene "high key") verso destra.
La maggior parte delle fotocamere hanno esposimetri interni che valutano l'illuminazione del soggetto e "tarano" in base a tale stima la luminosità della foto. Questa operazione tende a spostare i valori più alti verso i mezzi toni, e se generalmente il risultato è accettabile ci sono casi (vedi scene low ed high key) in cui andrebbero corretti manualmente. La consultazione degli istogrammi in queste situazione è dunque cosa buona e giusta per ottenere gli effetti voluti.
Gamma
La gamma di un monitor (a tubi catodici o LCD che sia) rappresenta quel fattore di non linearità che lega input e output dell'immagine, dove per input si intende il livello di luminosità dei pixel e per output il valore con cui viene visualizzato su schermo. Più precisamente, la gamma è l'esponente a cui bisogna elevare il valore di ingresso per ottenere quello d'uscita. In formula:
output = input gamma
Il valore di gamma standard è 2.2 , adottato da PAL e NTSC (due codifiche di trasmissione video), e corrisponde più o meno all'inverso della risposta umana. Il sistema operativo Windows tara il monitor via software su questo valore, mentre ad esempio Macintosh lo fissa a 1.8.
Per avere un'idea, se prendiamo un'immagine scattata da una fotocamera che applica una correzione di gamma a 2,2 e provassimo a visualizzarla su un monitor con risposta lineare (gamma 1), ciò che vedremmo sarebbe una foto troppo luminosa e con poca profondità.
Ribaltando il punto di vista, considerando cioè non più il momento della visualizzazione ma quello dell'acquisizione, se scattiamo una foto con gamma pari a 1 ed una col valore standard, sui nostri monitor la prima apparirà più scura della seconda.
Gamma dinamica
Per gamma dinamica di un sensore si intende il rapporto tra il segnale più grande e quello più piccolo che può registrare. Il valore massimo è direttamente proporzionale alle capacità del pixel, mentre quello più basso, essendo generato nella situazione di assenza di esposizione, può essere considerato il livello del rumore.
Sulla base delle considerazioni fatte nel capitolo precedente sulla gamma, prima di andare avanti sottolineiamo un concetto: il soggetto di una foto ha una propria gamma dinamica, la fotocamera ne ha un'altra, lo schermo un'altra ancora e - ovviamente - anche l'occhio ne ha una sua. Sono tutte uguali? Ovviamente no.
Le macchine fotografiche con un'ampia gamma dinamica, ad esempio le reflex, sono in grado di catturare maggiori dettagli sia nelle zone in ombra che in quelle più luminose. Tale caratteristica è strettamente collegata alle maggiori dimensioni dei loro pixel, per i motivi che abbiamo visto nel primo capitolo della prima parte.
Riprendiamo ora gli esempi visti nel paragrafo sugli istogrammi e commentiamoli considerando la loro gamma dinamica:
- nel primo caso la gamma dinamica della fotocamera è riuscita a catturare quella della scena, ed infatti dall'istogramma notiamo come sia i dettagli in ombra che in luce intensa siano garantiti
- nel secondo e terzo caso abbiamo una gamma dinamica della fotocamera limitata, la prima per problemi di sottoesposizione, la seconda per sovraesposizione
- nel quarto caso la gamma dinamica della fotocamera è inferiore a quella della scena, ed infatti perdiamo dettagli sia nelle zone scure che in quelle chiare
- nel quinto caso la gamma dinamica della fotocamera è superiore a quella della scena
Nelle fotocamere la gamma dinamica viene comunemente misurata in f-stop, quindi in potenze di 2. Ad esempio una gamma dinamica di 14 f-stop significa un contrasto di 16384:1, dove 16384 e 1 rappresentano il numero massimo e minimo di fotoni che possono essere raccolti dai pixel. L'occhio umano può vedere su una gamma di quasi 24 f-stop, motivo per cui si adatta così facilmente alla situazione ambientale e per cui è difficile fare foto piacevoli.
La gamma dinamica registrabile dipende anche dalla precisione con cui i fotodiodi traducono in digitale le misurazioni della quantità di luce. Per intenderci, 8 bit di precisione equivalgono a 8 f-stop (256 livelli di luminosità possibili), 12 bit equivalgono a 12 f-stop (la profondità di colore più comune per il formato raw, che arriva a rappresentare ben 4096 livelli diversi). Questi sono solo i valori teorici, che non tengono conto dei limiti posti dal rumore; in realtà il massimo che ci si può aspettare da una fotocamera è una gamma dinamica che va dai 5 ai 9 f-stop.
Perché nel paragrafo precedente abbiamo parlato di gamma dinamica "registrabile"? Perché anche partendo da immagini a 8 bit è possibile visualizzare foto con gamme dinamiche ampissime, applicando curve tonali o con la tecnica dell'HDR.
Gamma tonale
La gamma tonale corrisponde al numero di toni usati per descrivere la gamma dinamica, dove per tono si intende il livello di saturazione di un colore o della scala di grigi.
Gamma tonale e dinamica, spesso oggetto di confusione, sono strettamente collegate:
La gamma tonale può essere pensata come l’insieme delle molte gradazioni di grigio (compresi il nero puro e il bianco puro) rappresentate nell’immagine finale. L’esposimetro lavora privilegiando i toni medi. Se inquadrate quello che per voi è un muro bianchissimo - o all’opposto un pezzo di carbone nero come la notte - l’esposimetro calcolerà (o cercherà di farlo) una esposizione tale per cui quell’oggetto apparirà di un grigio medio, il cosiddetto “grigio al 18%” (in bianconero, la tonalità di grigio di un qualsiasi oggetto che riflette il 18% della luce che lo colpisce).
Curve
Abbiamo visto nel capitolo sulla linearità dei sensori che la comprensione e manipolazione delle curve è molto importante per l'intervento sui toni e sul contrasto dell'immagine.
Ricordiamo che le curve sono una rappresentazione grafica del rapporto tra la luce in ingresso (asse x) e la risposta in uscita (asse y), e che quella del sensore di una macchina fotografica non è altro che una diagonale a 45° che passa per il centro, motivo per cui si parla di risposta lineare.
I software delle fotocamere e molti programmi di fotoritocco consentono di modificare l'aspetto delle curve, e noteremo come aumentando o diminuendo la pendenza di quella lineare l'immagine visualizzata cambi – e molto – toni e contrasto.
Facciamo ora una serie di esempi illustrativi. Abbiamo la seguente immagine di partenza, di cui mostriamo anche la curva tonale e l'istogramma:
In questo caso abbiamo una perfetta risposta lineare, ovvero i valori di input corrispondono a quelli di output. Anticipiamo che la pendenza della curva è proprio la gamma, e che maggiore è il suo valore e più contrastata è l'immagine.
Cominciamo ad intervenire sulla luminosità: spostiamo il punto centrale della curva verso sinistra.
Trascinando il punto centrale verso sinistra abbiamo rimappato i punti della curva in modo che la maggior parte di essi si trovino nella metà superiore dell'output, con la conseguenza che l'immagine appare più chiara.
Adesso invece spostiamo il punto centrale della curva verso destra.
L'immagine in questo caso è diventata più scura perché il rimappaggio dei punti della sua curva ha traslato la maggior parte di essi nella metà inferiore dell'output, quindi a bassi valori di luminosità.
Interveniamo ora sul contrasto trascinando gli estremi della curva (i punti in alto a destra e in basso a sinistra) muovendoli orizzontalmente verso il centro, come effettuato qui sotto.
Come già anticipato, aumentando la pendenza della curva aumenta anche il contrasto dell'immagine. Notare dall'istogramma come questo tipo di curva abbia saturato agli estremi, con la conseguente perdita di dettagli nelle zone in ombra e in quelle più luminose.
Intuitivamente, per diminuire il contrasto dovremo spostare gli estremi della curva verticalmente verso il centro.
Notiamo come la pendenza della curva sia diminuita, e come di conseguenza anche la gamma dinamica si sia ridotta: i neri non sono più così neri e i bianchi non sono più così bianchi, si tende ovunque al grigio.
Come fare per intervenire sul contrasto senza perdere dettagli? La soluzione è tener conto anche dei mezzi toni. Per farlo fissiamo alcuni valori di riferimento sull'asse x: 64, 128, 192. Aumentiamo ora la pendenza della curva iniziale (quella lineare), spostando le coordinate a questi nuovi valori: (64,32) – (128,128) – (192,223). Ecco il risultato:
Cosa è successo? E' aumentato il contrasto dell'immagine, ed infatti nell'istogramma i picchi si sono spostati verso gli estremi (zone in ombra e quelle brillanti) appiattendosi nella parte centrale, ma senza eccessiva saturazione. La curva ottenuta è chiamata S-curva, ed aumenta il dettaglio dei mezzitoni riducendo il contrasto nelle zone più chiare e più scure, rendendo la percezione dell'immagine più vicina a quella dell'occhio umano.
Cambiamo ancora le coordinate della curva in: (32,64) – (128,128) – (223,192).
L'effetto stavolta è di una diminuzione del contrasto dell'immagine, con conseguente appiattimento dei valori agli estremi dell'istogramma e picchi maggiori nei mezzitoni. La curva ottenuta è chiamata S-curva invertita, ed aumenta i dettagli delle zone in luce e in ombra.
Dagli esempi visti possiamo trarre almeno altre due conclusioni. Anzitutto va detto che le curve (a meno che non abbiano pendenza negativa) garantiscono sempre la gerarchia tonale: se tra due toni ce n'è uno più luminoso, questo rimarrà tale anche dopo la manipolazione della curva (seppur con minore o maggiore differenza).
Notiamo poi che la pendenza della curva non influisce solo sul contrasto, ma anche sulla saturazione del colore; una S-Curve ha colori più saturi di una S-Curve invertita. Come possiamo sfruttare questa caratteristica? E' presto detto. Finora abbiamo lavorato sia sugli istogrammi che sulle curve tonali considerando tutti e tre i colori RGB insieme, ma gli stessi strumenti possono essere applicati ad un singolo canale per volta. Mettiamo allora che ho una foto con le zone più scure bluastre: se vado a diminuire la pendenza della curva del blu nella zona dei toni scuri posso risolvere (o comunque attenuare) il problema.
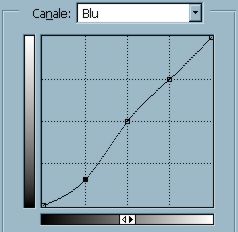Intervento sulla curva del bluCURVA CARATTERISTICA
La curva caratteristica sotto riportata e stata elaborata dagli studi di Hurter e Driffield, per cui la curva e anche chiamata H&D.
Essa e semplicemente un diagramma che presenta gli effetti di ogni grado di esposizione (ascisse) su un determinato materiale sensibile alla luce, come aumento di densità (ordinate), sono rappresentati ogni valore di esposizione, dalla sottoesposizione completa fino alla completa sovraesposizione.
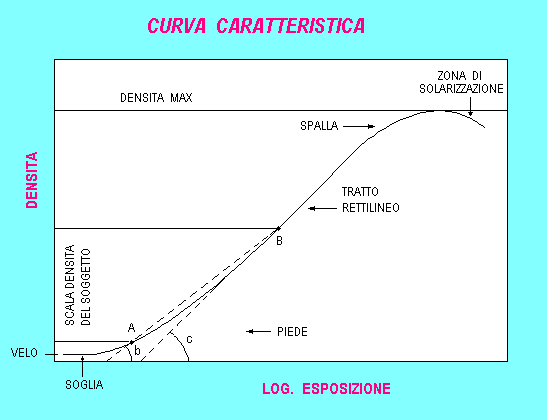Curva caratteristica H&Dle info (se c'entrano qualcosa con la nostra curva) sono qui
http://www.gulliver.it/bianconero/curva_ca.htm
Torna all'introduzione - Vai alla parte 1
Guide
